题目内容
已知函数g(x)=sin(x+
),f(x)=2cosx•g(x)-
(1)求函数f(x)的最小正周期及其对称中心坐标;
(2)当x∈[0,
]时,求函数f(x)的值域;
(3)由y=sinx可以按照如下变换得到函数y=f(x),y=sinx
y=sin(x+
)
y=sin(2x+
),写出①②的过程.
| π |
| 6 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期及其对称中心坐标;
(2)当x∈[0,
| π |
| 2 |
(3)由y=sinx可以按照如下变换得到函数y=f(x),y=sinx
| ① |
| π |
| 6 |
| ② |
| π |
| 6 |
分析:利用两角和与差的三角函数以及二倍角公式化简函数的表达式为一个角的一个三角函数的形式.
(1)直接求函数f(x)的最小正周期及其对称中心坐标;
(2)通过x∈[0,
],求出相位的范围,利用三角函数的值域求函数f(x)的值域;
(3)由y=sinx可以按照如下变换得到函数y=f(x),y=sinx
y=sin(x+
)
y=sin(2x+
),利用利用左加右减的原则,写出变换过程即可.
(1)直接求函数f(x)的最小正周期及其对称中心坐标;
(2)通过x∈[0,
| π |
| 2 |
(3)由y=sinx可以按照如下变换得到函数y=f(x),y=sinx
| ① |
| π |
| 6 |
| ② |
| π |
| 6 |
解答:解:函数g(x)=sin(x+
),f(x)=2cosx•g(x)-
=
sin2x+
cos2x=sin(2x+
).
(1)函数f(x)的最小正周期T=π,因为2x+
=kπ,所以对称中心坐标(
-
,0).k∈Z.
(2)x∈[0,
],2x+
∈[
,
],所以sin(2x+
)∈[-
,1].
函数f(x)的值域[-
,1],
(3)由y=sinx可以按照如下变换得到函数y=f(x),y=sinx
y=sin(x+
)
y=sin(2x+
),
①函数的图象向左平移
,②函数图象纵坐标不变,横坐标缩短为原来的
.
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(1)函数f(x)的最小正周期T=π,因为2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
(2)x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
函数f(x)的值域[-
| 1 |
| 2 |
(3)由y=sinx可以按照如下变换得到函数y=f(x),y=sinx
| ① |
| π |
| 6 |
| ② |
| π |
| 6 |
①函数的图象向左平移
| π |
| 6 |
| 1 |
| 2 |
点评:本题考查三角函数的化简求值,两角和与差的三角函数,三角函数的图象与性质,函数的图象的变换,基本知识的考查.

练习册系列答案
相关题目
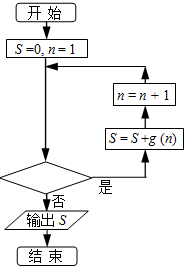 (2012•杭州二模)已知函数
(2012•杭州二模)已知函数