题目内容
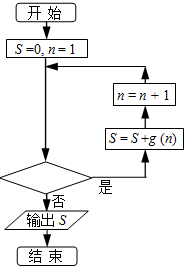 (2012•杭州二模)已知函数f(x)=ax3+
(2012•杭州二模)已知函数f(x)=ax3+| 1 |
| 2 |
| 1 |
| f′(x) |
| 2011 |
| 2012 |
分析:由f(x)在x=-1处取得极大值可得f′(-1)=0,由此可求得a值,则g(x)=
=
,g(n)=
=
-
,输出的结果S=g(1)+g(2)+…+g(n)=1-
+
-
+…+
-
=
,令S>
可得n>2011,即n=2012时S开始大于
,结合选项可得答案.
| 1 |
| f′(x) |
| 1 |
| x2+x |
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
| 2011 |
| 2012 |
| 2011 |
| 2012 |
解答:解:f′(x)=3ax2+x,
因为f(x)在x=-1处取得极大值,
所以f′(-1)=0,即3a-1=0,解得a=
,
故f′(x)=x2+x,则g(x)=
=
,
g(n)=
=
-
,
该循环结构为当型循环结构,选项C、D显然不正确,
输出的结果S=g(1)+g(2)+…+g(n)=1-
+
-
+…+
-
=
,
由S>
,得
>
,解得n>2011,
所以n=2012时S开始大于
,
故判断框中可以填入的关于n的判断条件为:n≤2012?,
故选B.
因为f(x)在x=-1处取得极大值,
所以f′(-1)=0,即3a-1=0,解得a=
| 1 |
| 3 |
故f′(x)=x2+x,则g(x)=
| 1 |
| f′(x) |
| 1 |
| x2+x |
g(n)=
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
该循环结构为当型循环结构,选项C、D显然不正确,
输出的结果S=g(1)+g(2)+…+g(n)=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
由S>
| 2011 |
| 2012 |
| n |
| n+1 |
| 2011 |
| 2012 |
所以n=2012时S开始大于
| 2011 |
| 2012 |
故判断框中可以填入的关于n的判断条件为:n≤2012?,
故选B.
点评:本题考查函数在某点取得极值的条件及程序框图,考查学生对题目的阅读理解能力及解决问题的能力.

练习册系列答案
相关题目
 (2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为
(2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为