题目内容
对n∈N?不等式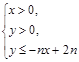 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2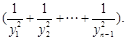 证明:当n≥2时,
证明:当n≥2时,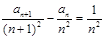 ;
;
(3)在(2)的条件下,试比较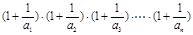 与4的大小关系.
与4的大小关系.
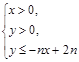 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2
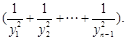 证明:当n≥2时,
证明:当n≥2时,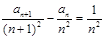 ;
;(3)在(2)的条件下,试比较
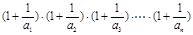 与4的大小关系.
与4的大小关系.(1)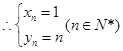
(2)运用整体的思想,作差法来得到化简证明。
(3)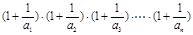 <4
<4
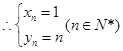
(2)运用整体的思想,作差法来得到化简证明。
(3)
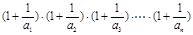 <4
<4试题分析:解:(1)当n=1时,(x1,y1)=(1,1)
n=2时,(x2,y2)="(1,2)" (x3,y3)=(1,3)
n=3时,(x4,y4)=(1,4)
n时 (xn,yn)=(1,n)
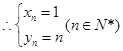
(2)由
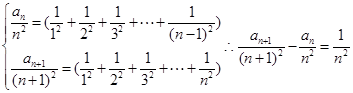
(3)当n=1时,
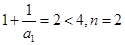 时,
时,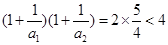 成立
成立由(2)知当n≥3时,
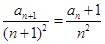 即
即

=
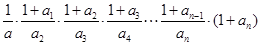
=
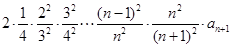
=
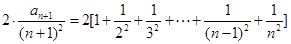
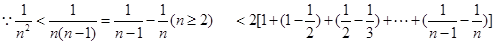
=
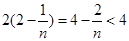 得证
得证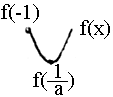
点评:对于数列与不等式结合的证明试题,是个难点,一般要用到放缩法来证明,需要同学们注意积累相关的放缩的方法。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
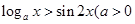 且
且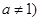 对任意
对任意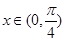 都成立,则
都成立,则 的取值
的取值



 满足
满足 ,则下列关系中不可能成立的是( )
,则下列关系中不可能成立的是( )



 ,则a,b,c的大小关系是 .
,则a,b,c的大小关系是 . 、
、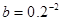 、
、 ,则有
,则有
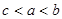


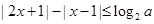 (其中
(其中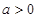 )。
)。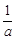 )(b+
)(b+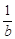 )≥
)≥ .
. 满足
满足 ,且有
,且有
