题目内容
已知过函数f(x)=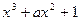 的图象上一点B(1,b)的切线的斜率为-3.
的图象上一点B(1,b)的切线的斜率为-3.
(1)求a、b的值;
(2)求A的取值范围,使不等式f(x)≤A-1987对于x∈[-1,4]恒成立;
令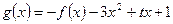 .是否存在一个实数t,使得当
.是否存在一个实数t,使得当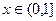 时,g(x)有最大值1?
时,g(x)有最大值1?
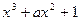 的图象上一点B(1,b)的切线的斜率为-3.
的图象上一点B(1,b)的切线的斜率为-3.(1)求a、b的值;
(2)求A的取值范围,使不等式f(x)≤A-1987对于x∈[-1,4]恒成立;
令
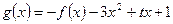 .是否存在一个实数t,使得当
.是否存在一个实数t,使得当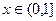 时,g(x)有最大值1?
时,g(x)有最大值1?(1)a=-3,b=-1;(2)存在一个a=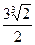 ,使g(x)在
,使g(x)在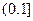 上有最大值1.
上有最大值1.
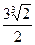 ,使g(x)在
,使g(x)在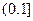 上有最大值1.
上有最大值1. (1)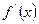 =
=
依题意得k= =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3
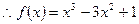 ,把B(1,b)代入得b=
,把B(1,b)代入得b=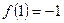
∴a=-3,b=-1
(2)令 =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987
∴A≥2004.
已知g(x)=-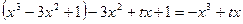
∴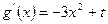
∵0<x≤1,∴-3≤-3x2<0,
当t>3时,t-3x2>0, ∴g(x)在
∴g(x)在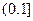 上为增函数,
上为增函数,
g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)
当0≤t≤3时,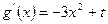
令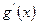 =0,得x=
=0,得x=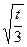
列表如下:
g(x)在x=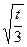 处取最大值-
处取最大值-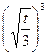 +t
+t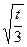 =1
=1
∴t=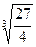 =
=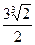 <
<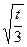 3
3
∴x=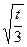 <1
<1
③当t<0时,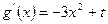 <0,∴g(x)在
<0,∴g(x)在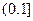 上为减函数,
上为减函数,
∴g(x)在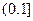 上为增函数,
上为增函数,
∴存在一个a=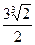 ,使g(x)在
,使g(x)在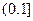 上有最大值1.
上有最大值1.
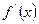 =
=
依题意得k=
 =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3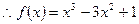 ,把B(1,b)代入得b=
,把B(1,b)代入得b=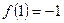
∴a=-3,b=-1
(2)令
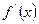 =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987
∴A≥2004.
已知g(x)=-
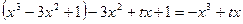
∴
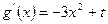
∵0<x≤1,∴-3≤-3x2<0,
当t>3时,t-3x2>0,
 ∴g(x)在
∴g(x)在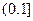 上为增函数,
上为增函数,g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)
当0≤t≤3时,
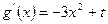
令
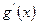 =0,得x=
=0,得x=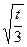
列表如下:
| x | (0, 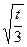 ) ) | 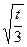 | 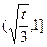 |
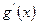 | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
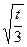 处取最大值-
处取最大值-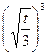 +t
+t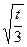 =1
=1∴t=
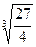 =
=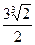 <
<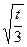 3
3∴x=
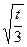 <1
<1③当t<0时,
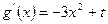 <0,∴g(x)在
<0,∴g(x)在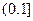 上为减函数,
上为减函数,∴g(x)在
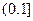 上为增函数,
上为增函数,∴存在一个a=
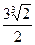 ,使g(x)在
,使g(x)在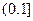 上有最大值1.
上有最大值1.
练习册系列答案
相关题目
 )与时间(
)与时间(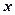 )的函数关系式;
)的函数关系式;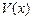 。
。
 上的最大值为2,求n的取值范围.
上的最大值为2,求n的取值范围.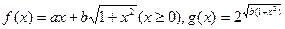 ,且
,且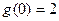 ,
,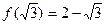 .
.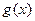 的值域
的值域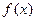 的单调性(不需证明),并求解关于实数
的单调性(不需证明),并求解关于实数 的不等式
的不等式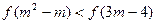 ;
;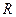 上的函数
上的函数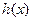 满足
满足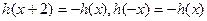 ,且当
,且当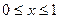 时
时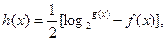 求方程
求方程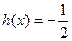 在区间
在区间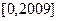 上的解的个数.
上的解的个数.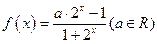 是R上的奇函数。
是R上的奇函数。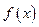 的反函数;
的反函数; ,解不等式:
,解不等式: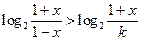
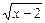 +
+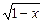 ;
;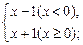 ④y=
④y=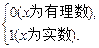
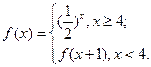 则
则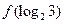 = .
= .