题目内容
设数列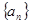 的前项n和为
的前项n和为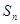 ,若对于任意的正整数n都有
,若对于任意的正整数n都有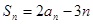 .
.
(1)求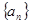 的通项公式。
的通项公式。
(2)求数列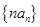 的前n项和.
的前n项和.
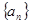 的前项n和为
的前项n和为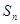 ,若对于任意的正整数n都有
,若对于任意的正整数n都有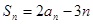 .
.(1)求
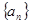 的通项公式。
的通项公式。(2)求数列
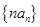 的前n项和.
的前n项和.(1)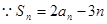 对于任意的正整数都成立,
对于任意的正整数都成立, 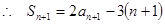
两式相减,得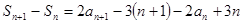
∴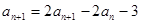 , 即
, 即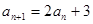
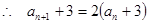 ,即
,即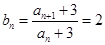 对一切正整数都成立。
对一切正整数都成立。
∴数列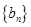 是等比数列。由已知得
是等比数列。由已知得 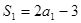 即
即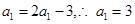
∴数列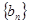 的首项
的首项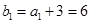 ,公比
,公比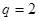 ,
,
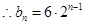 。
。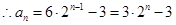 。
。
(2)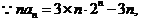
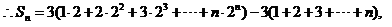




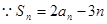 对于任意的正整数都成立,
对于任意的正整数都成立, 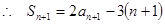
两式相减,得
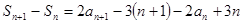
∴
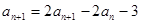 , 即
, 即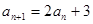
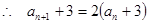 ,即
,即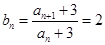 对一切正整数都成立。
对一切正整数都成立。∴数列
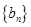 是等比数列。由已知得
是等比数列。由已知得 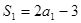 即
即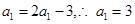
∴数列
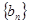 的首项
的首项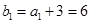 ,公比
,公比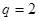 ,
,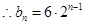 。
。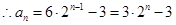 。
。(2)
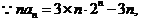
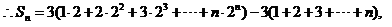




略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
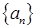 的前
的前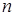 项和为
项和为 ,且
,且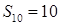 ,
, ,则
,则 ;
;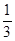 )是函数
)是函数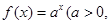 且
且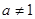 )的图象上一点,等比数列
)的图象上一点,等比数列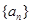 的前
的前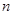 项和为
项和为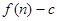 ,数列
,数列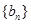
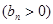 的首项为
的首项为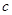 ,且前
,且前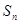 满足
满足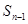 =
=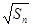 +
+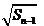 (
(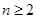 ).
).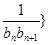 前
前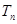 ,问
,问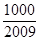 的最小正整数
的最小正整数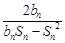 =1(n≥2).
=1(n≥2).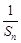 }成等差数列,并求数列{bn}的通项公式;
}成等差数列,并求数列{bn}的通项公式;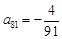 时,求上表中第k(k≥3)行所有项的和.
时,求上表中第k(k≥3)行所有项的和.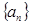 的前
的前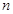 项和为
项和为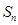 ,点
,点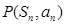 在直线
在直线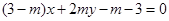 上,(
上,(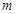 为常数,
为常数,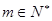 ,
,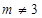 ).
).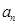 ;
;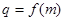 ,数列
,数列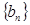 满足
满足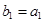 ,
,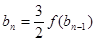 ,
,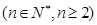 ,求证:
,求证: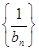 为等差数列,并求
为等差数列,并求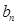 ;
;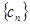 满足
满足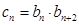 ,
,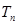 为数列
为数列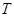 满足
满足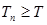
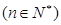 ,求
,求 的前n项和为
的前n项和为 ,且
,且
 求
求



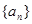 和
和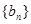 ,其前
,其前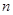 项和分别为
项和分别为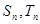 ,且
,且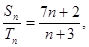 则
则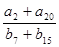 等于( )
等于( )


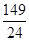




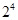
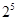



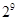
 行从左向右的第
行从左向右的第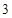 个数为 .
个数为 .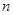 项和为286,则项数
项和为286,则项数