题目内容
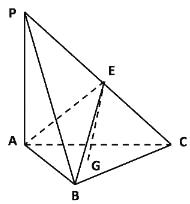
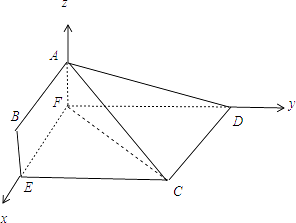
【题目】如图,四边形ABCD中,AB⊥CD,AD∥BC,AD=3,BC=2AB=2,E,F分别在BC,AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC.
(Ⅰ)若BE= ![]() ,在折叠后的线段AD上是否存在一点P,且
,在折叠后的线段AD上是否存在一点P,且 ![]() ,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
,使得CP∥平面ABEF?若存在,求出λ的值,若不存在,说明理由;
(Ⅱ)求三棱锥A﹣CDF的体积的最大值,并求此时二面角E﹣AC﹣F的余弦值.
【答案】解:(Ⅰ)∵平面ABEF⊥平面EFDC,平面ABEF∩平面EFDC=EF,
FD⊥EF,
∴FD⊥平面ABEF,又AF平面ABEF,
∴FD⊥AF,
在折起过程中,AF⊥EF,同时FD∩EF=F,
∴AF⊥平面EFDC,
以F为坐标原点,分别以FE,FD,FA所在直线为x,y,z轴,建立空间直角坐标系,
当BE= ![]() 时,F(0,0,0),A(0,0,
时,F(0,0,0),A(0,0, ![]() ),D(0,
),D(0, ![]() ,0),C(1,
,0),C(1, ![]() ,0),
,0),
平面ABEF的法向量 ![]() =(0,
=(0, ![]() ,0),
,0),
∵ ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() +
+ ![]() =
= ![]() ,
,
∴P(0, ![]() ,
, ![]() ),
),
∴ ![]() =(﹣1,
=(﹣1, ![]() ,
, ![]() ),
),
∵CP∥平面ABEF,∴ ![]() =
= ![]() =0,
=0,
解得 ![]() ,
,
∴线段AD上点P(0, ![]() ),且
),且 ![]() ,使得CP∥平面ABEF.
,使得CP∥平面ABEF.
(Ⅱ)设BE=x,则AF=x(0<x≤2),FD=3﹣x,
∴VA﹣CDF= ![]() =
= ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,VA﹣CDF有最大值,且最大值为
时,VA﹣CDF有最大值,且最大值为 ![]() ,
,
∴A(0,0, ![]() ),C(1,
),C(1, ![]() ,0),D(0,
,0),D(0, ![]() ,0),E(1,0,0),
,0),E(1,0,0),
∴ ![]() =(1,0,﹣
=(1,0,﹣ ![]() ),
), ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() ),
), ![]() =(0,0,
=(0,0, ![]() ),
), ![]() =(1,
=(1, ![]() ,0),
,0),
设平面AEC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 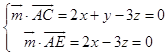 ,取x=3,得
,取x=3,得 ![]() =(3,0,2),
=(3,0,2),
设平面ACF的一个法向量 ![]() =(a,b,c),
=(a,b,c),
则 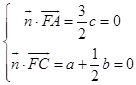 ,取a=1,得
,取a=1,得 ![]() =(1,﹣2,0),
=(1,﹣2,0),
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
∴二面角E﹣AC﹣F的余弦值为 ![]() .
.
【解析】(Ⅰ)推导出FD⊥EF,FD⊥AF,以F为坐标原点,分别以FE,FD,FA所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出线段AD上存在点P(0, ![]() ),
), ![]() ,使得CP∥平面ABEF.(Ⅱ)设BE=x,则AF=x(0<x≤2),FD=3﹣x,推导出当x=
,使得CP∥平面ABEF.(Ⅱ)设BE=x,则AF=x(0<x≤2),FD=3﹣x,推导出当x= ![]() 时,VA﹣CDF有最大值,且最大值为
时,VA﹣CDF有最大值,且最大值为 ![]() ,求出此时平面AEC的一个法向量和平面ACF的一个法向量,利用向量法能求出二面角E﹣AC﹣F的余弦值.
,求出此时平面AEC的一个法向量和平面ACF的一个法向量,利用向量法能求出二面角E﹣AC﹣F的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案