题目内容
已知直线y＝k(x＋1)与抛物线y2＝－x相交于A、B两点，O为坐标原点，当△OAB的面积为
时，求k的值．
答案：
解析：
解析：
|
解：S△OAB＝ k2x2＋(2k2＋1)x＋k2＝0． 由韦达定理得x1＋x2＝－ 由弦长公式得|AB|＝ ＝ 而原点到直线的距离d＝ ∴S△OAB＝ 分析：当直线与抛物线相交时，得到一条弦，本题实质上是以△OAB的面积来考查弦长公式． |
|AB|·d，其中d表示原点到直线AB的距离．把直线方程代入抛物线方程，化简得
，x1x2＝1．
·|x1－x2|
．
，
＝
，∴k＝±
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，有如下信息：联立方程组
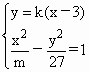消去y后得到方程Ax2＋Bx＋C＝0，分类讨论：
，0)．
)与抛物线C交于A、B两点，且|FA|＝2|FB|，求k的值；