题目内容
2.已知数列{an},则“an,an+1,an+2,(n∈N*)”成等比数列是“an+12=anan+2”的( )| A. | 既不充分也不必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 充要条件 |
分析 根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可.
解答 解:若an,an+1,an+2(n∈N+)成等比数列,则an+12=anan+2成立,
当an=an+1=an+2=0时,满足an+12=anan+2成立,但an,an+1,an+2(n∈N*)成等比数列不成立,‘
故an,an+1,an+2(n∈N*)成等比数列是“an+12=anan+2”的充分不必要条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,根据等比数列的性质是解决本题的关键.

练习册系列答案
相关题目
14.3对夫妇去看电影,6个人坐成一排,若女性的邻座只能是其丈夫或其他女性,则坐法的种数为( )
| A. | 54 | B. | 60 | C. | 66 | D. | 72 |
 与圆切于点
与圆切于点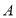 ,过
,过 作直线与圆交于
作直线与圆交于 两点,点
两点,点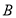 在圆上,且
在圆上,且 .
.
 ;
; ,求
,求 .
. 如图,CD是圆O的切线,切点为D,CA是过圆心的割线且交圆O于B点,过B作⊙O的切线交CD于点E,DE=$\frac{1}{2}$EC.求证:
如图,CD是圆O的切线,切点为D,CA是过圆心的割线且交圆O于B点,过B作⊙O的切线交CD于点E,DE=$\frac{1}{2}$EC.求证: