题目内容
将正方形ABCD沿对角线BD折成直二面角 ,有如下四个结论:
,有如下四个结论:
①AC⊥BD;② 是等边三角形;③
是等边三角形;③ 与
与 所成的角为
所成的角为 ;④
;④ 与平面
与平面 成
成 的角。
的角。
其中正确的结论的序号是 .
.
 ,有如下四个结论:
,有如下四个结论:①AC⊥BD;②
 是等边三角形;③
是等边三角形;③ 与
与 所成的角为
所成的角为 ;④
;④ 与平面
与平面 成
成 的角。
的角。其中正确的结论的序号是
 .
.①②③
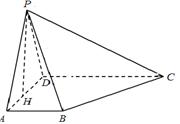
试题分析:根据已知中正方形ABCD沿对角线BD折成直二面角,我们以O点为坐标原点建立空间坐标系,求出ABCD各点坐标后,进而可以求出相关直线的方向向量及平面的法向量,然后代入线线夹角,线面夹角公式,及模长公式,分别计算即可得到答案.解:连接AC与BD交于O点,对折后如图所示,令OC=1

则O(0,0,0),A(1,0,0),B(0,1,0),C(0,0,1),D(0,-1,0)可知向量AC垂直与向量BD,故可知①正确,同时利用两点的距离公式得到AD=DC=CA,故该三角形是等边三角形,成立,对于
 与
与 所成的角为
所成的角为 ;根据向量的夹角公式得到成立,而
;根据向量的夹角公式得到成立,而 与平面
与平面 成
成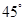 的角。故填写①②③
的角。故填写①②③点评:本题以平面图形的翻折为载体,考查空间中直线与平面之间的位置关系,根据已知条件构造空间坐标系,将空间线线夹角,线面夹角转化为向量的夹角问题是解题的关键

练习册系列答案
相关题目
 矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证:
矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证: 平面
平面

 中,
中,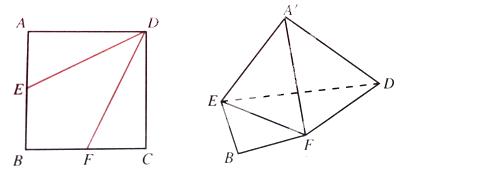
 是
是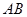 的中点,点
的中点,点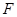 是
是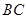 的中点,将
的中点,将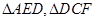 分别沿
分别沿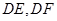 折起,使
折起,使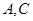 两点重合于点
两点重合于点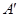 。求证:
。求证: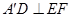
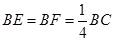 时,求三棱锥
时,求三棱锥 的体积。
的体积。 的底面是菱形,且
的底面是菱形,且 面
面 ,
, ,
, ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点,
的中点,
 面
面 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; 的体积.
的体积.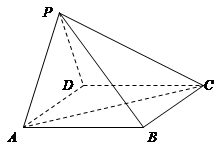
 的棱线长为1,面对角线
的棱线长为1,面对角线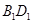 上有两个动点E,F,且
上有两个动点E,F,且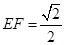 ,则下列四个结论中①
,则下列四个结论中①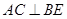 ②
②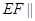 平面
平面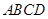 ③三棱锥
③三棱锥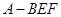 的体积为定值 ④异面直线
的体积为定值 ④异面直线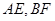 所成的角为定值,其中正确的个数是
所成的角为定值,其中正确的个数是 ,AB=2CD=8.
,AB=2CD=8.
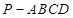 中,
中,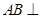 平面
平面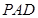 ,
,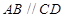 ,
,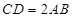 ,
,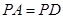 ,
, 是
是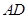 的中点.
的中点.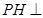 平面
平面 ;
;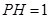 ,
,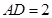 ,
,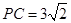 ,求二面角
,求二面角 的正切值.
的正切值.