题目内容
如图,已知棱柱 的底面是菱形,且
的底面是菱形,且 面
面 ,
, ,
, ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点,
的中点,

(Ⅰ)求证: 面
面 ;
;
(Ⅱ)判断直线 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(Ⅲ)求三棱锥 的体积.
的体积.
 的底面是菱形,且
的底面是菱形,且 面
面 ,
, ,
, ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点,
的中点,
(Ⅰ)求证:
 面
面 ;
;(Ⅱ)判断直线
 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;(Ⅲ)求三棱锥
 的体积.
的体积.(Ⅰ)证明:连结 、
、 交于点
交于点 ,再连结
,再连结 ,
,
可得 且
且 ,四边形
,四边形 是平行四边形,由
是平行四边形,由 ,
, 平面
平面 .
.
(Ⅱ) 平面
平面
(Ⅲ) .
.
 、
、 交于点
交于点 ,再连结
,再连结 ,
,可得
 且
且 ,四边形
,四边形 是平行四边形,由
是平行四边形,由 ,
, 平面
平面 .
.(Ⅱ)
 平面
平面
(Ⅲ)
 .
.试题分析:(Ⅰ)证明:连结
 、
、 交于点
交于点 ,再连结
,再连结 ,
,
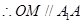 ,且
,且 , 又
, 又 ,故
,故 且
且 ,
, 四边形
四边形 是平行四边形,故
是平行四边形,故 ,
, 平面
平面 4分
4分(Ⅱ)
 平面
平面 ,下面加以证明:
,下面加以证明:在底面菱形
 中
中 ,
, 又
 平面
平面 ,
, 面
面
 ,
, 平面
平面 ,
,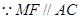 ,
, 平面
平面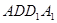 8分
8分(Ⅲ)过点
 作
作 ,垂足
,垂足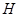 ,
, 平面
平面 ,
, 平面
平面
 ,
, 平面
平面 ,
,在
 中,
中, ,
, ,故
,故
 ,
, 12分
12分点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。本题含“探究性问题”,这一借助于几何体中的垂直关系。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
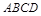 为梯形,
为梯形,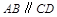 ,
,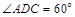 ,四边形
,四边形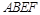 为矩形,且平面
为矩形,且平面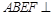 平面
平面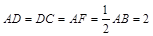 ,点
,点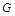 为
为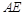 的中点.
的中点.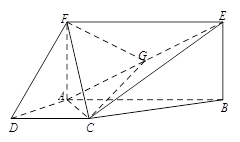
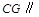 平面
平面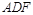 ;
;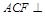 平面
平面 ;
;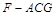 的体积.
的体积.



 ,则线段
,则线段 的中点
的中点 的坐标为 ( )
的坐标为 ( )

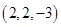

 为正方形,面
为正方形,面 为等腰梯形,
为等腰梯形, ,
, ,
, ,
, .
.
 ;
; 的体积;
的体积;  上是否存在点
上是否存在点 ,使
,使 //平面
//平面 ?证明你的结论.
?证明你的结论.
 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 、
、 外的一个动点,
外的一个动点, 平面
平面 ,
, ,
, ,
, ,
, .
.
 平面
平面 ;
; 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值. ,有如下四个结论:
,有如下四个结论: 是等边三角形;③
是等边三角形;③ 与
与 所成的角为
所成的角为 ;④
;④ 成
成 .
.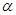 的一条斜线,O为斜足,OB为OA在平面
的一条斜线,O为斜足,OB为OA在平面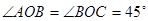 ,则
,则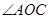 的大小为( )
的大小为( )


