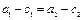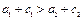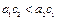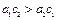题目内容
给出下列曲线:
①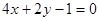 ;②
;② 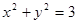 ;③
;③ 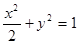 ;④
;④ 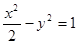 .
.
其中与直线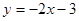 有公共点的所有曲线是 ( )
有公共点的所有曲线是 ( )
①
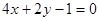 ;②
;② 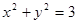 ;③
;③ 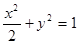 ;④
;④ 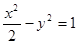 .
.其中与直线
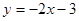 有公共点的所有曲线是 ( )
有公共点的所有曲线是 ( )| A.①③ | B.②④ | C.①②③ | D.②③④ |
D
分析:先看①中直线的斜率与直线y=-2x-3相等可判断两直线平行,不可能有交点.进而把直线方程与②③④中的曲线方程联立消去y,进而根据△大于0可判定与他们均有交点.
解答:解:∵直线y=-2x-3和4x+2y-1=0 的斜率都是-2
∴两直线平行,不可能有交点.
把直线y=-2x-3与x2+y2=3联立消去y得5x2+12x+6=0,△=144-120>0,∴直线与②中的曲线有交点.
把直线y=-2x-3与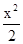 +y2=1联立消去y得9x2+24x+12=0,△=24×24-18×24>0,直线与③中的曲线有交点.
+y2=1联立消去y得9x2+24x+12=0,△=24×24-18×24>0,直线与③中的曲线有交点.
把直线y=-2x-3与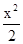 -y2=1联立消去y得7x2-24x-12=0,△=24×24+4×7×12>0,直线与④中的曲线有交点.
-y2=1联立消去y得7x2-24x-12=0,△=24×24+4×7×12>0,直线与④中的曲线有交点.
故选D
解答:解:∵直线y=-2x-3和4x+2y-1=0 的斜率都是-2
∴两直线平行,不可能有交点.
把直线y=-2x-3与x2+y2=3联立消去y得5x2+12x+6=0,△=144-120>0,∴直线与②中的曲线有交点.
把直线y=-2x-3与
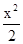 +y2=1联立消去y得9x2+24x+12=0,△=24×24-18×24>0,直线与③中的曲线有交点.
+y2=1联立消去y得9x2+24x+12=0,△=24×24-18×24>0,直线与③中的曲线有交点.把直线y=-2x-3与
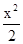 -y2=1联立消去y得7x2-24x-12=0,△=24×24+4×7×12>0,直线与④中的曲线有交点.
-y2=1联立消去y得7x2-24x-12=0,△=24×24+4×7×12>0,直线与④中的曲线有交点.故选D

练习册系列答案
相关题目
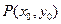 、
、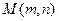 是圆锥曲线C上不与顶点重合的任意两点,
是圆锥曲线C上不与顶点重合的任意两点, 是垂直于
是垂直于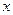 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线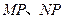 分别交
分别交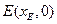 和点
和点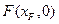 。
。
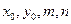 的代数式分别表示
的代数式分别表示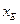
 和
和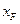 ;
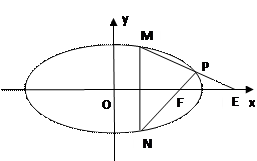
;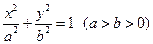 (如图),求证:
(如图),求证: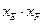 是与
是与 位置无关的定值;
位置无关的定值;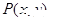 是曲线
是曲线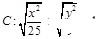 上的点,
上的点,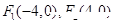 ,则
,则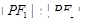 ( )
( )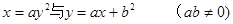 的图像只可能是下图中( *** )
的图像只可能是下图中( *** )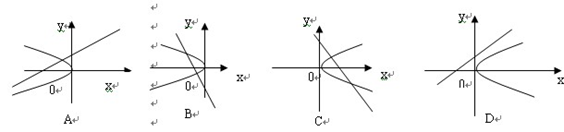
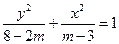 表示曲线C.
表示曲线C.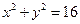 上任一点连线的中点轨迹方程是
上任一点连线的中点轨迹方程是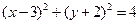
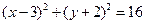
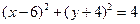
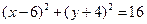
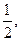 求点M的轨迹方程。
求点M的轨迹方程。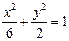 和双曲线
和双曲线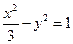 的公共点为
的公共点为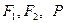 是两曲线的一个交点, 那么
是两曲线的一个交点, 那么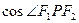 的值是___________
的值是___________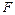 的椭圆Ⅰ与Ⅱ的长半轴的长分别为
的椭圆Ⅰ与Ⅱ的长半轴的长分别为 和
和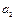 ,半焦距分别为
,半焦距分别为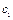 和
和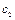 ,则下列结论不正确的是( )
,则下列结论不正确的是( )