题目内容
在数列{an}中，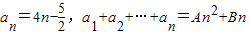
，n∈N*，其中A，B为常数，则A，B的积AB等于 ．
【答案】分析：判定数列为等差数列，根据首项的值和数列的前n项之和，根据对应系数相等可得结果．
解答：解：a1=4×1-
=
，又an+1-an=4（n+1）-
-4n+
=4，
故数列{an}为等差数列，
∴Sn=
=2n2-
n，
又Sn=An2+Bn，∴A=2，B=-
，
∴AB=-1．
故答案为：-1．
点评：本题考查等差数列的基本量的关系，考查等差数列的性质，属基础题．
解答：解：a1=4×1-
=，又an+1-an=4（n+1）--4n+=4，故数列{an}为等差数列，
∴Sn=
=2n2-n，又Sn=An2+Bn，∴A=2，B=-
，∴AB=-1．
故答案为：-1．
点评：本题考查等差数列的基本量的关系，考查等差数列的性质，属基础题．
练习册系列答案
华东师大版一课一练系列答案
相关题目