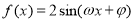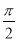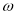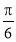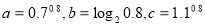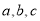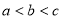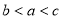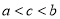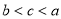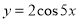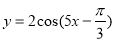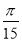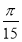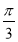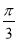题目内容
已知函数 和函数
和函数 ,其中
,其中 为参数,且满足
为参数,且满足 .
.
(1)若 ,写出函数
,写出函数 的单调区间(无需证明);
的单调区间(无需证明);
(2)若方程 在
在 上有唯一解,求实数
上有唯一解,求实数 的取值范围;
的取值范围;
(3)若对任意 ,存在
,存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1) 的单调增区间为
的单调增区间为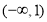 ,
, ,单调减区间为
,单调减区间为 ;(2)
;(2) 或
或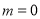 ;(3)
;(3) .
.
【解析】
试题分析:(1)当 时,
时, ,由二次函数的图像与性质可写出函数
,由二次函数的图像与性质可写出函数 的单调区间;(2)先将
的单调区间;(2)先将 在
在 上有唯一解转化为
上有唯一解转化为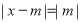 在
在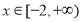 上有唯一解,进而两边平方得到
上有唯一解,进而两边平方得到 或
或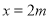 ,要使
,要使 时,有唯一解,则只须
时,有唯一解,则只须 或
或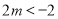 即可,问题得以解决;(3)对任意
即可,问题得以解决;(3)对任意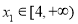 ,存在
,存在 ,使得
,使得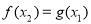 成立的意思就是
成立的意思就是 的值域应是
的值域应是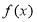 的值域的子集,然后分别针对
的值域的子集,然后分别针对 与
与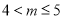 两种情形进行讨论求解,最后将这两种情况求解出的
两种情形进行讨论求解,最后将这两种情况求解出的 的取值范围取并集即可.
的取值范围取并集即可.
试题解析:(1) 时,
时, 1分
1分
函数 的单调增区间为
的单调增区间为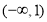 ,
, ,单调减区间为
,单调减区间为 4分
4分
(2)由 在
在 上有唯一解
上有唯一解
得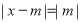 在
在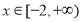 上有唯一解 5分
上有唯一解 5分
即 ,解得
,解得 或
或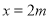 6分
6分
由题意知 或
或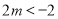
即 或
或
综上, 的取值范围是
的取值范围是 或
或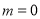 8分
8分
(3)
则 的值域应是
的值域应是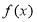 的值域的子集 9分
的值域的子集 9分
① 时,
时, 在
在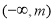 上单调递减,
上单调递减, 上单调递增,故
上单调递增,故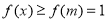 10分
10分
 在
在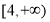 上单调递增,故
上单调递增,故 11分
11分
所以 ,即
,即 12分
12分
②当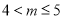 时,
时, 在
在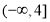 上单调递减,故
上单调递减,故
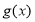 在
在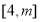 上单调递减,
上单调递减,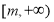 上单调递增,故
上单调递增,故
所以 ,解得
,解得 .又
.又 ,所以
,所以 13分
13分
综上, 的取值范围是
的取值范围是 14分.
14分.
考点:1.二次函数的图像与性质;2.指数函数的图像与性质;3.函数的单调性与最值.

练习册系列答案
相关题目