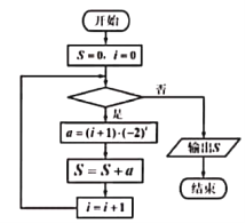
题目内容
【题目】已知![]() 是正项数列
是正项数列![]() 的前
的前![]() 项和,
项和,![]() ,
,![]() .
.
(1)证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,
,
①求证:![]() ;
;
②解关于![]() 的不等式:
的不等式:![]() .
.
【答案】(1)见解析;(2)①见解析;②![]() ,
,![]()
【解析】
(1)运用数列的递推式,结合等差数列的定义和通项公式,可得所求;
(2)①![]() ,运用数列的错位相减法求和,结合等比数列的求和公式和不等式的性质,即可得证;
,运用数列的错位相减法求和,结合等比数列的求和公式和不等式的性质,即可得证;
②原不等式化为![]() ,即
,即![]() ,运用二项式定理和不等式的性质,可得解集.
,运用二项式定理和不等式的性质,可得解集.
(1)证明:![]() 是正项数列
是正项数列![]() 的求和,
的求和,![]() ,
,![]() ,
,
可得![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,又
,又![]() ,
,
两式相减可得![]() ,
,
化为![]() ,
,
由正项数列![]() ,可得
,可得![]() ,
,
可得数列![]() 是首项和公差均为1的等差数列;
是首项和公差均为1的等差数列;
(2)①证明:![]() ,前
,前![]() 项和
项和![]() ,
,
![]() ,
,
两式相减可得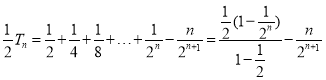 ,
,
化为![]() ,
,
可得![]() ;
;
②![]() 即
即![]() ,
,
化为![]() ,即
,即![]() ,
,
![]() ,
,
可得![]() 时
时![]() ;
;![]() 时,
时,![]() ;
;![]() 不成立,
不成立,
故原不等式的解集为![]() ,
,![]() .
.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
【题目】某家庭记录了未使用节水龙头30天的日用水量数据(单位:![]() )和使用了节水龙头30天的日用水量数据,得到频数分布表如下:
)和使用了节水龙头30天的日用水量数据,得到频数分布表如下:
(一)未使用节水龙头30天的日用水量频数分布表
日用水量 |
|
|
|
|
|
频数 | 2 | 3 | 8 | 12 | 5 |
(二)使用了节水龙头30天的日用水量频数分布表
日用水量 |
|
|
|
|
|
频数 | 2 | 5 | 11 | 6 | 6 |
(1)估计该家庭使用了节水龙头后,日用水量小于![]() 的概率;
的概率;
(2)估计该家庭使用节水龙头后,平均每天能节省多少水?(同一组中的数据以这组数据所在区间中点的值作代表)