题目内容
已知向量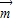 =(sinωx,1),
=(sinωx,1),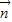 =(
=(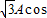 ωx,
ωx,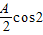 ωx)(A>0,ω>0),函数f(x)=
ωx)(A>0,ω>0),函数f(x)= 的最大值为3,且其图象相邻两条对称轴之间的距离为π.
的最大值为3,且其图象相邻两条对称轴之间的距离为π.(I)求函数f(x)的解析式;
(II)将函数y=f(x)的图象向左平移
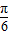 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.
倍,纵坐标不变,得到函数y=g(x)的图象.(1)求函数g(x)的单调递减区间;
(2)求函数g(x)在
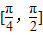 上的值域.
上的值域.
【答案】分析:(I)利用两个向量的数量积的定义、三角函数的恒等变换,化简函数f(x)的解析式为Asin(2ωx+ ),由最大值求得A,由周期求出ω,从而确定函数f(x)的解析式.
),由最大值求得A,由周期求出ω,从而确定函数f(x)的解析式.
(II)根据y=Asin(ωx+∅)的图象变换规律 求出函数g(x)=3sin(2x+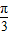 ).(1)由2kπ+
).(1)由2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,求得x的范围,即可求得g(x)的单调递减区间.
,求得x的范围,即可求得g(x)的单调递减区间.
(2)当x的范围,求得2x+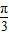 的范围,可得sin(2x+
的范围,可得sin(2x+ )的范围,从而求得g(x)的范围.
)的范围,从而求得g(x)的范围.
解答:解:(I)函数f(x)= =
=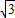 Asinωxcosωx+
Asinωxcosωx+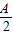 cos2ωx=A(
cos2ωx=A(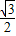 sinωxcosωx+
sinωxcosωx+ cos2ωx)=Asin(2ωx+
cos2ωx)=Asin(2ωx+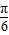 ),…(3分)
),…(3分)
因为函数f(x)的最大值为3,且其图象相邻两条对称轴之间的距离为π,
所以A=3,函数的周期T=2π,又 T= ,所以ω=
,所以ω= . …(5分)
. …(5分)
所以 f(x)=3sin(x+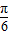 ). …(6分)
). …(6分)
(II)将函数y=f(x)的图象向左平移 个单位,得到函数 y=3sin[(x+
个单位,得到函数 y=3sin[(x+ )+
)+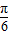 ]的图象,
]的图象,
再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数g(x)=3sin(2x+
倍,纵坐标不变,得到函数g(x)=3sin(2x+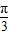 )的图象. …(8分)
)的图象. …(8分)
(1)因为函数y=sinx 的单调递减区间为[2kπ+ ,2kπ+
,2kπ+ ],(k∈z ),
],(k∈z ),
所以 2kπ+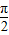 ≤2x+
≤2x+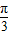 ≤2kπ+
≤2kπ+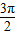 ,解得 kπ+
,解得 kπ+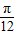 ≤x≤kπ+
≤x≤kπ+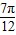 ,
,
所以函数g(x)的单调递减区间为[kπ+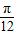 ,kπ+
,kπ+ ],(k∈z).…(11分)
],(k∈z).…(11分)
(2)当x∈[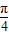 ,
,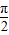 ]时,2x+
]时,2x+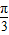 ∈[
∈[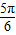 ,
, ],sin(2x+
],sin(2x+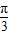 )∈[-
)∈[-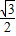 ,
, ],g(x)∈[-
],g(x)∈[- ,
, ].
].
所以函数g(x)在[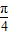 ,
, ]上的值域为[-
]上的值域为[-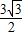 ,
, ]. …(14分)
]. …(14分)
点评:本题主要考查两个向量的数量积的定义,三角函数的恒等变换及化简求值,y=Asin(ωx+∅)的图象变换规律,正弦函数的定义域和值域、单调性,属于中档题.
 ),由最大值求得A,由周期求出ω,从而确定函数f(x)的解析式.
),由最大值求得A,由周期求出ω,从而确定函数f(x)的解析式.(II)根据y=Asin(ωx+∅)的图象变换规律 求出函数g(x)=3sin(2x+
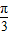 ).(1)由2kπ+
).(1)由2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,求得x的范围,即可求得g(x)的单调递减区间.
,求得x的范围,即可求得g(x)的单调递减区间.(2)当x的范围,求得2x+
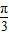 的范围,可得sin(2x+
的范围,可得sin(2x+ )的范围,从而求得g(x)的范围.
)的范围,从而求得g(x)的范围.解答:解:(I)函数f(x)=
 =
=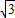 Asinωxcosωx+
Asinωxcosωx+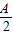 cos2ωx=A(
cos2ωx=A(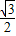 sinωxcosωx+
sinωxcosωx+ cos2ωx)=Asin(2ωx+
cos2ωx)=Asin(2ωx+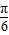 ),…(3分)
),…(3分)因为函数f(x)的最大值为3,且其图象相邻两条对称轴之间的距离为π,
所以A=3,函数的周期T=2π,又 T=
 ,所以ω=
,所以ω= . …(5分)
. …(5分)所以 f(x)=3sin(x+
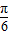 ). …(6分)
). …(6分)(II)将函数y=f(x)的图象向左平移
 个单位,得到函数 y=3sin[(x+
个单位,得到函数 y=3sin[(x+ )+
)+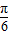 ]的图象,
]的图象,再将所得图象上各点的横坐标缩短为原来的
 倍,纵坐标不变,得到函数g(x)=3sin(2x+
倍,纵坐标不变,得到函数g(x)=3sin(2x+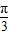 )的图象. …(8分)
)的图象. …(8分)(1)因为函数y=sinx 的单调递减区间为[2kπ+
 ,2kπ+
,2kπ+ ],(k∈z ),
],(k∈z ),所以 2kπ+
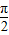 ≤2x+
≤2x+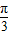 ≤2kπ+
≤2kπ+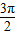 ,解得 kπ+
,解得 kπ+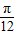 ≤x≤kπ+
≤x≤kπ+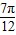 ,
,所以函数g(x)的单调递减区间为[kπ+
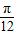 ,kπ+
,kπ+ ],(k∈z).…(11分)
],(k∈z).…(11分)(2)当x∈[
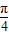 ,
,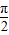 ]时,2x+
]时,2x+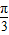 ∈[
∈[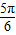 ,
, ],sin(2x+
],sin(2x+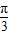 )∈[-
)∈[-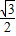 ,
, ],g(x)∈[-
],g(x)∈[- ,
, ].
].所以函数g(x)在[
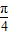 ,
, ]上的值域为[-
]上的值域为[-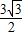 ,
, ]. …(14分)
]. …(14分)点评:本题主要考查两个向量的数量积的定义,三角函数的恒等变换及化简求值,y=Asin(ωx+∅)的图象变换规律,正弦函数的定义域和值域、单调性,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目