Question

直线y=kx+3与圆（x-3）²+（y-2）²=4相交于M，N两点，若|MN|≥2

3

，则k的取值范围是（　　）

• A、[-

  3

  4

  ，0]
• B、(-∞，-

  3

  4

  ]∪[0，+∞)
• C、[-

  3

  3

  ，

  3

  3

  ]
• D、[-

  2

  3

  ，0]

Answer 1

分析：先求圆心坐标和半径，求出最大弦心距，利用圆心到直线的距离不大于最大弦心距，求出k的范围．

解答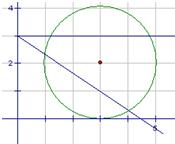：解：解法1：圆心的坐标为（3，2），且圆与x轴相切．
当|MN|=2

3

时，弦心距最大，
由点到直线距离公式得

|3k-2+3|

1+k2

≤1
解得k∈[-

3

4

，0]；
故选A．

解法2：数形结合，如图由垂径定理得夹在两直线之间即可，不取+∞，排除B，考虑区间不对称，排除C，利用斜率估值，
故选A．

点评：考查直线与圆的位置关系、点到直线距离公式，重点考查数形结合的运用．解法2是一种间接解法，选择题中常用．