题目内容
(1)如图(a)(b)(c)(d)为四个平面图,数一数,每个平面图各有多少个顶点?多少条边?它们将平面围成了多少个区域?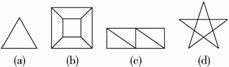
| 顶点数 | 边数 | 区域数 |
(a) |
|
|
|
(b) |
|
|
|
(c) |
|
|
|
(d) |
|
|
|
(2)观察上表,推断一个平面图形的顶点数、边数、区域数之间有什么关系?
(3)现已知某个平面图有999个顶点,且围成了999个区域,试根据以上关系确定这个平面图有多少条边?
解:(1)各平面图形的顶点数\,边数\,区域数分别为
(a)3、3、2;
(b)8、12、6;
(c)6、9、5;
(d)10、15、7.
(2)观察:3+2-3=2,
8+6-12=2,
6+5-9=2,
10+7-15=2.
通过观察发现,它们的顶点数V、边数E、区域数F之间的关系为V+F-E=2.
(3)由已知V=999,F=999,代入上述关系式,得E=1 996,故这个平面图有1 996条边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
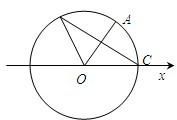 如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.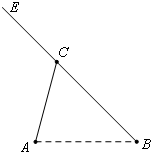 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.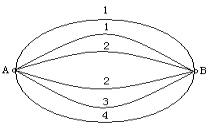 如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中任取三条网线且使每条网线通过最大信息量.
如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中任取三条网线且使每条网线通过最大信息量. 如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=
如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=