题目内容
如图，在三棱锥A﹣BCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．
（1）求证：四边形EFGH是平行四边形；
（2）若AC=BD，求证：四边形EFGH是菱形；
（3）当AC与BD满足什么条件时，四边形EFGH是正方形．
（1）求证：四边形EFGH是平行四边形；
（2）若AC=BD，求证：四边形EFGH是菱形；
（3）当AC与BD满足什么条件时，四边形EFGH是正方形．
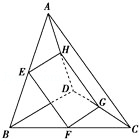
解：（1）证明：在△ABC中，E、F分别是边AB、BC中点，
所以EF∥AC，且EF=
AC，
同理有GH∥AC，且GH=
AC，
∴EF∥GH且EF=GH，
故四边形EFGH是平行四边形．
（2）证明：仿（1）中分析，EH∥BD且EH=
BD，
若AC=BD，则有EH=EF，
又因为四边形EFGH是平行四边形，
∴四边形EFGH是菱形．
（3）当AC=BD且AC⊥BD时，
四边形EFGH是正方形．
所以EF∥AC，且EF=
AC，同理有GH∥AC，且GH=
AC，∴EF∥GH且EF=GH，
故四边形EFGH是平行四边形．
（2）证明：仿（1）中分析，EH∥BD且EH=
BD，若AC=BD，则有EH=EF，
又因为四边形EFGH是平行四边形，
∴四边形EFGH是菱形．
（3）当AC=BD且AC⊥BD时，
四边形EFGH是正方形．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
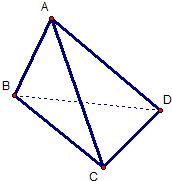如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=
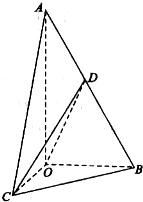如图，在三棱锥A-BOC中，AO⊥底面BOC，∠OAB=∠OAC=30°，AB=AC=4，
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．
如图，在三棱锥A-BOC中，AO⊥面BOC，二面角B-AO-C是直二面角，OB=OC，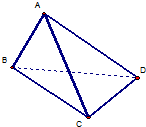
如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=