题目内容

16．分别判断下列直线是否相交，若相交，求出它们的交点．
（Ⅰ）l1：2x-y=7和l2：3x+2y-7=0
（Ⅱ）l1：2x-6y+4=0和l2：4x-12y-8=0．

分析 利用两条直线平行的条件进行判断，通过解方程组求出交点坐标．

解答 解：（Ⅰ）l1：2x-y=7和l2：3x+2y-7=0，
∵2×2≠（-1）×3，
∴两条直线相交，
解方程组$\left\{\begin{array}{l}{2x-y=7}\\{3x+2y-7=0}\end{array}\right.$，可得交点坐标（3，-1）；
（Ⅱ）l1：2x-6y+4=0和l2：4x-12y-8=0．
∵2×（-12）=（-6）×4，
∴两条直线平行．

点评 本题考查两条直线的位置关系，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
4．已知函数f（x）=x3-3ax2+3bx，其中b＞0．
（1）若函数f（x）在区间（0，+∞）上是增函数，求证：a≤$\sqrt{b}$；
（2）若函数f（x）在点（1，f（1））处的切线方程是y=4x-1，试求a、b的值．
7．如图，圆O的内接△ABC中，M是BC的中点，AC=3，AB=$\sqrt{7}$，则$\overrightarrow{AO}•\overrightarrow{AM}$=4．
4．已知|$\overrightarrow{a}$|=6，|$\overrightarrow{b}$|=4，$\overrightarrow{a}$•$\overrightarrow{b}$=-12$\sqrt{2}$，求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ．
11．某教育网站需要老师为其命制试题，组建题库，已知吴老师、王老师、张老师三位老师命制的试题数分别为350道，700道、1050道，现用分层抽样的方法随机抽取6道试题进行科学性，严密性，正确性检验．
（1）求从吴老师、王老师、张老师三位老师中分别抽取的试题的题数；
（2）从抽取的6道试题中任意取出2道，已知这2道试题都不是吴老师命制的，求其中至少有一道是王老师命制的概率．
1．甲乙两人分别从A城到B城，甲以速度v1走了一半的路程，以速度v2走了另一半的路程；乙的行程中有一半的时间速度为v1，另一半时间的速度为v2，比较甲、乙两人从A城到B城所需的时间大小．
8．在△ABC中，$\overrightarrow{AB}$=$\overrightarrow{a}$，AC=$\overrightarrow{b}$，$\overrightarrow{BC}$=$\overrightarrow{c}$，若$\overrightarrow{a}$•$\overrightarrow{a}$=$\overrightarrow{a}$•$\overrightarrow{b}$+（-$\overrightarrow{a}$）•$\overrightarrow{c}$+（-$\overrightarrow{a}$）•（-$\overrightarrow{c}$），试判断△ABC的形状．
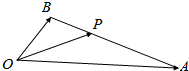5．如图，在△ABC中，已知P为线段AB上一点，且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$．
（1）若$\overrightarrow{AP}$=$\overrightarrow{PB}$，求x，y的值；
（2）若$\overrightarrow{AP}$=3$\overrightarrow{PB}$，|$\overrightarrow{OA}$|=4，|$\overrightarrow{OB}$|=2，且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°，求$\overrightarrow{OP}$$•\overrightarrow{AB}$的值．
6．已知在△ABC中，AB=2，BC=4，AC=3，若△ABC的内心为I，则$\overrightarrow{IA}$•$\overrightarrow{BC}$=-$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网