题目内容
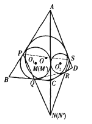
【题目】已知四边形ABCD外切于
，△ACB的内切圆
与边AB、BC的切点分别为P、Q，，△ACD的内切圆
与边CD、DA的切点分别为R、S. 求证：三条直线PQ、RS、AC共点或平行．
【答案】见解析
【解析】
记
、
与AC的切点分别为
、
由
、分别是△ACB、△ACD的内切圆知
又由四边形ABCD外切于
知AB+AD=CB+CD．从而，
这表明，点M与
重合．
若PQ∥AC，易知A、C两点关于直线BD对称，则RS∥AC.
于是，PQ、RS、AC互相平行.
若PQ
AC，则易知RSAC.
如图，记直线PQ、RS分别与直线AC交于点N、
对△ACB和截线PQN应用梅涅劳斯定理得
结合BP=BQ，得 
同理，
这表明，点N与重合，即PQ、RS、AC三线共点.
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】在2019年高考数学的全国Ⅲ卷中，文科和理科的选做题题目完全相同，第22题考查选修4-4：极坐标和参数方程；第23题考查选修4-5：不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式，在测试结束后，该校数学组教师对该校全体高三学生的选做题得分情况进行了统计，得到两题得分的
列联表如下（已知每名学生只做了一道题）：
选做22题 | 选做23题 | 合计 | |
文科人数 | 50 | 60 | |
理科人数 | 40 | ||
总计 | 400 |
（1）完善列联表中的数据，判断能否有
的把握认为“选做题的选择”与“文、理科的科类”有关；
（2）经统计，第23题得分为0的学生中，理科生占理科总人数的
，文科生占文科总人数的
，在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导，并在辅导后随机抽取2名学生进行测试，求被抽中进行测试的2名学生均为理科生的概率.
附：
，其中
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】大型综艺节目《最强大脑》中，有一个游戏叫做盲拧魔方，就是玩家先观察魔方状态并进行记忆，记住后蒙住眼睛快速还原魔方，盲拧在外人看来很神奇，其实原理是十分简单的，要学会盲拧也是很容易的.为了解某市盲拧魔方爱好者的水平状况，某兴趣小组在全市范围内随机抽取了
名魔方爱好者进行调查，得到的情况如表所示：
用时（秒） |
|
|
|
|
男性人数 | 15 | 22 | 14 | 9 |
女性人数 | 5 | 11 | 17 | 7 |
附：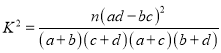
，
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
（1）将用时低于
秒的称为“熟练盲拧者”，不低于秒的称为“非熟练盲拧者”.请根据调查数据完成以下
列联表，并判断是否有
的把握认为是否为“熟练盲拧者”与性别有关？
熟练盲拧者 | 非熟练盲拧者 | |
男性 | ||
女性 |
（2）以这名盲拧魔方爱好者的用时不超过
秒的频率，代替全市所有盲拧魔方爱好者的用时不超过秒的概率，每位盲拧魔方爱好者用时是否超过秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取
名爱好者进行测试，其中用时不超过秒的人数最有可能（即概率最大）是多少？
