题目内容
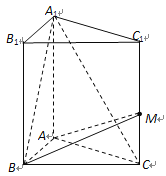
【题目】在正方体
中， 
、
分别是
、
的中点.
(1)求证：四边形
是菱形；
(2)求异面直线
与
所成角的大小 (结果用反三角函数值表示) .
【答案】(1)证明见解析；（2）
.
【解析】试题分析：（1）建立空间直角坐标系，如图所示：先证其是平行四边形，再根据空间向量模相等说明邻边相等即可；（2）可得
，利用空间向量夹角余弦公式可得结果.
试题解析：（1）设正方体的棱长为1，建立空间直角坐标系，如图所示：
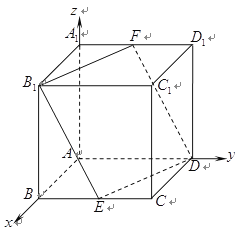
则
, 
, 
, 
,
所以
,即
且
,故四边形
是平行四边形
又因为
,所以
故平行四边形
是菱形
(2)因为
设异面直线
与
所成的角的大小为
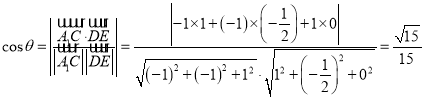
所以
, 故异面直线
与
所成的角的大小为
.
【方法点晴】本题主要考查异面直线所成的角以及空间向量的应用，属于难题.求异面直线所成的角主要方法有两种：一是向量法，根据几何体的特殊性质建立空间直角坐标系后，分别求出两直线的方向向量，再利用空间向量夹角的余弦公式求解；二是传统法，利用平行四边形、三角形中位线等方法找出两直线成的角，再利用平面几何性质求解.
练习册系列答案
相关题目
【题目】某车间为了规定工时定额，需要确定加工某零件所花费的时间，为此做了四次实验，得到的数据如表：
零件的个数x（个） | 2 | 3 | 4 | 5 |
加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出y关于x的线性回归方程y= 
x+ 
，并在坐标系中画出回归直线；
（3）试预测加工6个零件需要多少时间？
（注： = 
， = 
﹣ 
）
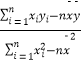