题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{2-(\frac{1}{3})^{x},x≤0}\\{\frac{1}{2}{x}^{2}-x+1,x>0}\end{array}\right.$.(1)请在直角坐标系中画出函数f(x)的图象,并写出该函数的单调区间;
(2)若方程f(x)-m=0恰有3个不同根,求实数m的取值范围.
分析 (1)利用函数的平移和二次函数的图象画出函数f(x)的图象;
(2)利用数学结合,方程问题转换为函数交点问题.
解答 解:(1)函数f(x)的图象如右图:
函数f(x)的单调减区间是(0,1)
单调增区间是(-∞,0)和(1,+∞)
(2)方程f(x)-m=0可变成m=f(x)
方程f(x)-m=0恰有3个不同根等价于函数y=m与函数f(x)的图象恰有三个不同公共点,由函数的图象知
m∈($\frac{1}{2}$,1).
点评 考察了函数图象的画法和方程问题的转换,是数形结合的典型题型.

练习册系列答案
相关题目
8.设x、y∈R,则命题“x2+y2>1”是命题“|x|+|y|>1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
4.不等式|x+2|+|x-3|≥m2-4m对任意实数x恒成立,则实数m的取值范围是( )
| A. | (1,5) | B. | [2,3) | C. | [-1,5] | D. | [-1,3] |
1.在△ABC中,角A、B、C所对的边分别为a,b,c若2acosB=c,则2cos2$\frac{A}{2}$+sinB-1的取值范围是 ( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | (-1,$\sqrt{2}$] |
18.在△ABC中,若sinA>sinB,则A与B的大小关系为( )
| A. | A、B的大小关系不确定 | B. | A=B | ||
| C. | A<B | D. | A>B |
19.比较a=2-3.1,b=0.53,c=log3.14,则a,b,c的大小关系是( )
| A. | c<b<a | B. | b<c<a | C. | a<c<b | D. | a<b<c |
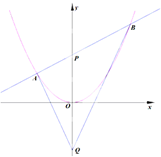 如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.
如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.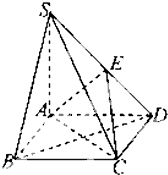 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.