题目内容
14.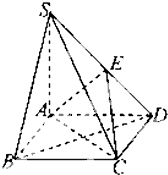 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.(1)证明:BD⊥平面SAC;
(2)问:侧棱SD上是否存在点E,使得SB∥平面ACE?请证明你的结论;若存在点E,求出ES的长度.
分析 (1)根据四棱锥S-ABCD底面是菱形,得到BD⊥AC且AD=AB,又SA2+AB2=SB2,SA2+AD2=SD2,根据三边满足勾股定理可知SA⊥AB,SA⊥AD,又AB∩AD=A,根据线面垂直的判定定理可知SA⊥平面ABCD,而BD?平面ABCD,从而SA⊥BD,又SA∩AC=A,满足定理条件,BD⊥平面SAC;
(2)在侧棱SD上存在点E,使得SB∥平面ACE,其中E为SD的中点,然后证明,设BD∩AC=O,则O为BD的中点,又E为SD的中点,连接OE,则OE为△SBD的中位线,则OE∥SB,又OE?平面AEC,SB?平面AEC,根据线面平行的判定定理可知SB∥平面ACE.
解答  解:(1)∵四棱锥S-ABCD底面是菱形,
解:(1)∵四棱锥S-ABCD底面是菱形,
∴BD⊥AC且AD=AB,
又SA=AB=2,SB=SD=2$\sqrt{2}$.
∴SA2+AB2=SB2,
SA2+AD2=SD2∴SA⊥AB,SA⊥AD,
又AB∩AD=A,
∴SA⊥平面ABCD,
BD?平面ABCD,从而SA⊥BD,
又SA∩AC=A,
∴BD⊥平面SAC.
(2)在侧棱SD上存在点E,使得SB∥平面ACE,其中E为SD的中点,
证明:设BD∩AC=O,则O为BD的中点,
又E为SD的中点,连接OE,
则OE为△SBD的中位线.
∴OE∥SB,
又OE?平面AEC,SB?平面AEC,
∴SB∥平面ACE.
∴ES=$\frac{1}{2}$SD=$\frac{1}{2}×2\sqrt{2}$=$\sqrt{2}$.
点评 本题主要考查了直线与平面垂直的判定,以及直线与平面平行的判定,同时考查了化归与转化的数学思想方法,以及空间想象能力、推理论证能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.$\lim_{n→∞}\frac{{n•{3^n}}}{{n{{(x-2)}^n}+n•{3^{n+1}}-{3^n}}}=\frac{1}{3}$则实数x的取值范围是( )
| A. | [-1,5] | B. | (-1,5) | C. | [-1,5] | D. | (-5,5) |
6.函数f(x)=1-xlnx的零点所在区间是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,2) |
3.240°的弧度数是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{7π}{6}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |