题目内容
已知曲线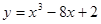
(1)求曲线在点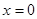 处的的切线方程;
处的的切线方程;
(2)过原点作曲线的切线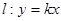 ,求切线方程.
,求切线方程.
(1)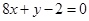 ;(2)
;(2)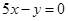 .
.
解析试题分析:
解题思路:(1)求导,得到切线的斜率,利用直线的点斜式方程写出切线方程,再化成一般式即可;(2)设切点坐标,求切线斜率,写出切线方程,代入(0,0)求 即可.
即可.
规律总结:利用导数的几何意义求的切线方程: .
.
注意点:要注意区分“在某点处的切线”与“过某点的切线”.
试题解析:(1)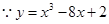 ,
,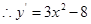 ,则
,则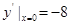 ,所以曲线在点
,所以曲线在点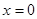 处的的切线方程为
处的的切线方程为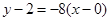 ,即
,即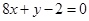 ;
;
设切点为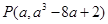 ,切线斜率
,切线斜率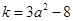 ;则切线方程
;则切线方程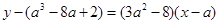 ,
,
又因为切线过原点,所以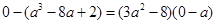 ,即
,即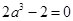 ,所以
,所以 ,即切线斜率为
,即切线斜率为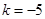 ,切线方程为
,切线方程为 ,即
,即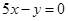 .
.
考点:导数的几何意义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
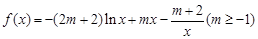 .
.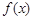 的单调性;
的单调性;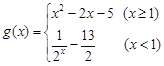 .当
.当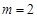 时,若对任意
时,若对任意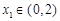 ,存在
,存在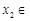
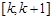 ,(
,(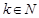 ),使
),使 ,求实数
,求实数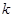 的最小值.
的最小值.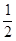 x2﹣2x﹣
x2﹣2x﹣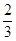 .
.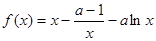
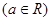 .
. 是函数
是函数 的极大值点,求
的极大值点,求 的取值范围;
的取值范围;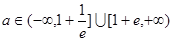 时,若在
时,若在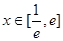 上至少存在一点
上至少存在一点 ,使
,使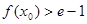 成立,求
成立,求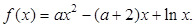
 在点
在点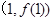 处的切线方程;
处的切线方程;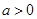 时,若
时,若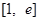 上的最小值为
上的最小值为 ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
. 在
在 处取得极值,求
处取得极值,求 内有极大值和极小值,求实数
内有极大值和极小值,求实数 的取值范围.
的取值范围.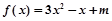 ,
,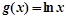 ,若函数
,若函数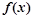 与
与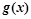 的图象在
的图象在 处的切线平行,则
处的切线平行,则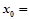 .
.  ,则
,则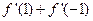 的值为___▲___.
的值为___▲___.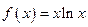 ,函数
,函数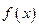 在
在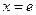 处的切线方程为 ;
处的切线方程为 ;