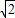题目内容
已知m2+n2=1,a2+b2=2,则am+bn的最大值是( )
| A.1 | B.
| C.
| D.以上都不对 |
三角代换:令m=cosθ,n=sinθ,a=
cosβ,b=
sinβ.
∴am+bn=
cosθcosβ+
sinθsinβ=
cos(θ-β)≤
,
故 am+bn的最大值是
,
故选 C.
| 2 |
| 2 |
∴am+bn=
| 2 |
| 2 |
| 2 |
| 2 |
故 am+bn的最大值是
| 2 |
故选 C.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
已知m2+n2=1,a2+b2=2,则am+bn的最大值是( )
| A、1 | ||
B、
| ||
C、
| ||
| D、以上都不对 |