题目内容
（本题13分）已知函数
．
（1）当
时，试比较
与1的大小；
（2）令g(x)=(x+1)f(x),若x＞1时，方程g(x)=a2无解。求a的范围；
（3）求证：
（
）．
解：（1）当
时，
，定义域为
．
令
，
，
在上是增函数．
①当
时，
，即
；
②当
时，
，即
；
③当
时，
，即
．
（2）g(x)=(x+1)f(x)= (x+1)lnx+a
g (x)=
＞0
∴g(x)在区间（1，+∞）上单调递增，
∴g (x)min＞ g (1)=a
∴a2≤a ∴a∈[0,1]
（3）根据（1）的结论，当时，
，即
．
令
，则有
， 
．……12分
，
． …………………………………14分
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
f (x) + sinx是区间[1，1]上的减函数．
t + 1在x∈[1，1]上恒成立，求t的取值范围；
的根的个数．
，
．
的最大值和最小值；（II）若不等式
在
的取值范围．
.
时，求
的单调区间；
单调增加，在
单调减少，证明：
＜6.
（1）当
时，判断函数
在其定义域内是否存在极值？若存在，求出极值，若不存在，说明理由（2）若函数
的取值范围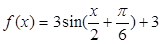
，
，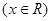
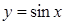