题目内容
设函数![]() ,已知
,已知![]() 是奇函数。
是奇函数。
(1)求![]() 、
、![]() 的值.
的值.
(2)求![]() 的单调区间与极值.
的单调区间与极值.
![]() ,
,![]() ,
,![]() 和
和![]() 是函数
是函数![]() 是单调递增区间;
是单调递增区间;
![]() 是函数
是函数![]() 是单调递减区间
是单调递减区间![]() 在
在![]() 时,取得极大值,极大值为
时,取得极大值,极大值为![]() ,
,
![]() 在
在![]() 时,取得极小值,极小值为
时,取得极小值,极小值为![]() .
.
解析:
解: (1)∵![]() ,
,
∴![]() .┈┈┈┈┈┈┈┈┈┈┈┈2分
.┈┈┈┈┈┈┈┈┈┈┈┈2分
从而![]()
=![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
是一个奇函数,
所以![]() 得
得![]() ,
,
由奇函数定义得![]() ; ┈┈┈┈┈┈┈┈┈┈┈┈4分
; ┈┈┈┈┈┈┈┈┈┈┈┈4分
(2)由(Ⅰ)知![]() ,从而
,从而![]() ,
,
由此可知,![]() 和
和![]() 是函数
是函数![]() 是单调递增区间;
是单调递增区间;
![]() 是函数
是函数![]() 是单调递减区间;┈┈┈┈┈┈┈4分
是单调递减区间;┈┈┈┈┈┈┈4分
![]() 在
在![]() 时,取得极大值,极大值为
时,取得极大值,极大值为![]() ,
,
![]() 在
在![]() 时,取得极小值,极小值为
时,取得极小值,极小值为![]() .┈┈┈┈┈4分
.┈┈┈┈┈4分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,已知
,已知 是奇函数。
是奇函数。 、
、 的值. (2)求
的值. (2)求 的单调区间与极值.
的单调区间与极值.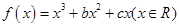 ,已知
,已知 是奇函数.
是奇函数. 、
、 的值; (Ⅱ)求
的值; (Ⅱ)求 的单调区间与极值.
的单调区间与极值.