题目内容
(06年安徽卷文)(12分)
设函数![]() ,已知
,已知![]() 是奇函数。
是奇函数。
(Ⅰ)求![]() 、
、![]() 的值。
的值。
(Ⅱ)求![]() 的单调区间与极值。
的单调区间与极值。
解析:证明(Ⅰ)∵![]() ,∴
,∴![]() 。从而
。从而![]() =
=![]() 是一个奇函数,所以
是一个奇函数,所以![]() 得
得![]() ,由奇函数定义得
,由奇函数定义得![]() ;
;
(Ⅱ)由(Ⅰ)知![]() ,从而
,从而![]() ,由此可知,
,由此可知,
![]() 和
和![]() 是函数
是函数![]() 是单调递增区间;
是单调递增区间;
![]() 是函数
是函数![]() 是单调递减区间;
是单调递减区间;
![]() 在
在![]() 时,取得极大值,极大值为
时,取得极大值,极大值为![]() ,
,![]() 在
在![]() 时,取得极小值,极小值为
时,取得极小值,极小值为![]() 。
。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 展开式中
展开式中 ,
, 展开式中
展开式中 的系数为
的系数为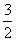 ,则
,则 =_____。
=_____。