题目内容
设函数
，已知
是奇函数。
（1）求
、
的值．（2）求
的单调区间与极值．
（1）
，
（2）
和
是函数是单调递增区间；
是函数是单调递减区间；极大值为
，极小值为
.
解析:
（1）∵
，∴
.┈┈2分
从而
＝
┈┈┈2分 是一个奇函数，所以
得
，由奇函数定义得
；┈4分
（2）由（Ⅰ）知
，从而
，由此可知，
和
是函数
是单调递增区间；
是函数是单调递减区间；┈4分
在
时，取得极大值，极大值为
，在
时，取得极小值，极小值为
.┈4分w.w.w.k.s.5.u.c.o.m 
练习册系列答案
智趣暑假温故知新系列答案
相关题目
，已知
是奇函数。
、
的值。
的单调区间与极值。
，已知
是奇函数。
、
的值。
的单调区间与极值。
，已知
是奇函数。
、
的值． （2）求
的单调区间与极值．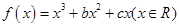
，已知
是奇函数.
、
的值; （Ⅱ）求
的单调区间与极值.