题目内容
已知矩阵M=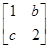 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1=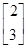 .求:
.求:
(1)矩阵M;
(2)曲线5x2+8xy+4y2=1在M的作用下的新曲线方程.
(1)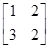 (2)x2+y2=2
(2)x2+y2=2
解析

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
题目内容
已知矩阵M=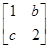 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1=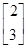 .求:
.求:
(1)矩阵M;
(2)曲线5x2+8xy+4y2=1在M的作用下的新曲线方程.
(1)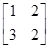 (2)x2+y2=2
(2)x2+y2=2
解析

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案