题目内容
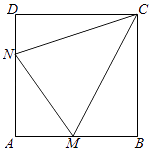
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)是否存在实数![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅱ)在 (Ⅰ)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)当![]() ,即
,即![]() 为
为![]() 中点时
中点时![]() 平面
平面![]() ,(2)
,(2)![]()
【解析】【试题分析】(1)运用线面平行的判定定理进行分析推证;(2)建立空间直角坐标系,运用空间向量的坐标形式的运算及空间向量的数量积公式进行求解:
解:(1)当![]() ,即
,即![]() 为
为![]() 中点时
中点时![]() 平面
平面![]() ,
,
取![]() 中点
中点![]() ,连
,连![]()
![]()

![]() 平面
平面![]()
![]()
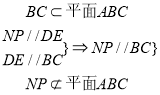
![]() 平面
平面![]()
所以,平面![]() 平面
平面![]() 平面
平面![]()
(2)取![]() 中点
中点![]() ,连
,连![]()

![]() 平面
平面![]() ,
,

![]()
以![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立直角坐标系
轴,建立直角坐标系
![]() ,
, ![]() ,
, ![]() ,
, 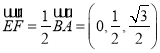 ,所以
,所以
 ,
, 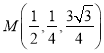 ,
, ![]()
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则
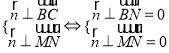

![]()
![]()
所以,直线![]() 与平面
与平面![]() 的正弦值为
的正弦值为![]()

 阅读快车系列答案
阅读快车系列答案【题目】2017年某市街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() 的被调查人中随机选取两人,对年龄在
的被调查人中随机选取两人,对年龄在![]() 的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:  ,其中
,其中![]() .
.