题目内容
已知数列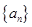 的前n项和
的前n项和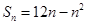
(1)求数列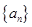 的通项公式,并证明
的通项公式,并证明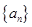 是等差数列;
是等差数列;
(2)若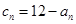 ,求数列
,求数列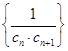 的前
的前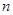 项和
项和 .
.
(1) 通项公式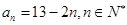 ,证明过程详见试题解析;(2)
,证明过程详见试题解析;(2)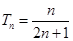 .
.
解析试题分析:(1) 先根据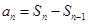 ,求出当
,求出当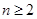 时
时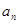 的表达式;再验证
的表达式;再验证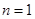 时是否满足;证明
时是否满足;证明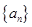 是等差数列,即证明
是等差数列,即证明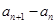 是定值即可;(2)先求出
是定值即可;(2)先求出 的表达式,再用裂项相消法求数列前n项和.
的表达式,再用裂项相消法求数列前n项和.
试题解析:(1)当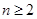 时,
时, 3分
3分
当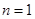 时,
时,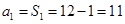 适合上式,所以
适合上式,所以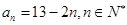 4分
4分
因为当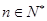 时,
时,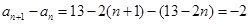 为定值,
为定值,
所以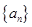 是等差数列 6分
是等差数列 6分
(2)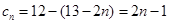 ,
,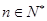
所以
所以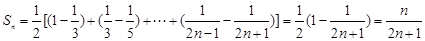 10分
10分
考点:数列通项公式的求和、数列求和.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
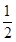 .
.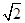 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.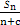 ,求非零常数c.
,求非零常数c.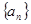 是等差数列,且
是等差数列,且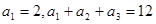
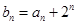 ,求数列
,求数列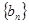 前n项和
前n项和
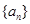 的前n项和为
的前n项和为 ,且
,且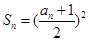 。
。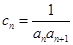 ,数列
,数列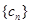 的前n项和为
的前n项和为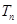 ,证明:
,证明: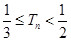 。
。