题目内容
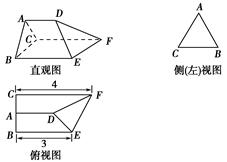
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.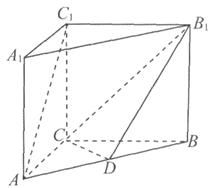
(1)求证:AC1∥平面CDB1;
(2)求三棱锥D-B1C1C的体积.
(1)证明过程详见试题解析;(2)三棱锥D-B1C1C的体积为 .
.
解析试题分析:(1)连接BC1,设BC1与B1C的交点为E,连接DE,证得DE∥AC1;由线面平行的判定定理即可证明AC1∥平面CDB1;(2)在平面ABC内作DF⊥BC于点F,可以证明DF是三棱锥D-CC1B1的高,再由锥体体积公式即可求解.
试题解析:
(1)证明:连接BC1,设BC1与B1C的交点为E,连接DE.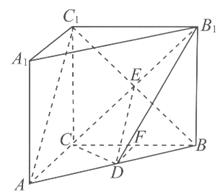
∵D是AB的中点,E是BC1的中点
∴DE∥AC1.
又∵DE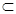 平面CDB1,AC1
平面CDB1,AC1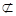 平面CDB1,
平面CDB1,
∴AC1∥平面CDB1. 4分
(2)在平面ABC内作DF⊥BC于点F,
∵C1C⊥平面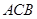 ,
,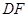
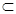 平面
平面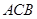 ,
,
∴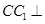
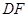 .
.
∴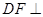 平面
平面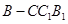 .
.
∴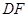 是三棱锥
是三棱锥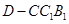 的高,
的高,
∵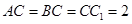
∴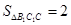 ,
,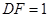 .
.
∴三棱锥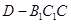 的体积为
的体积为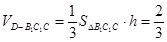 . 8分
. 8分
考点:线面平行的判定定理、空间几何体的体积.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

 为圆
为圆 的直径,点
的直径,点 .
.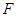 在圆
在圆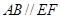 ,矩形
,矩形 所在的平面和圆
所在的平面和圆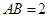 ,
,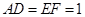 .
.
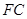 的中点为
的中点为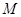 ,求证:
,求证: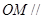 平面
平面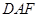 ;
; 的体积.
的体积.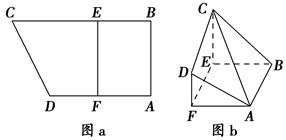
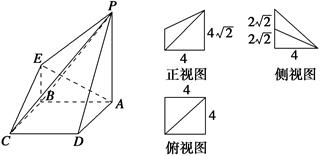
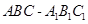 中,
中,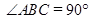 ,
,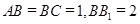 ,求:
,求: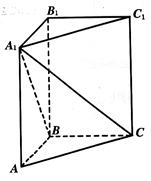
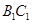 与
与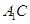 所成角的大小;
所成角的大小; 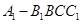 的体积.
的体积.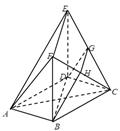
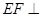 平面
平面 ,
, ,
,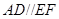 ,
,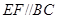 ,
,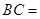
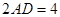 ,
,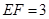 ,
,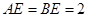 ,
,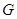 是
是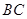 的中点.
的中点.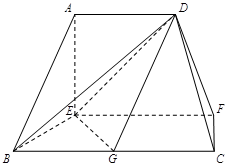
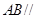 平面
平面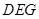 ;
;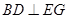 ;
; 的体积.
的体积.