题目内容
2.已知某商品的价格每上涨x%,销售的数量就减少$\frac{x}{2}$%.则该商品的价格上涨多少才能使销售的总金额最大?分析 通过设原销售额为a,列出涨价后销售额y关于x的表达式,进而配方计算即得结论.
解答 解:设原销售额为a,则涨价后销售额y=a(1+x%)(1-$\frac{x}{2}$%)=a(1+$\frac{x}{200}$-$\frac{{x}^{2}}{20000}$),
整理得:y=-$\frac{a}{20000}$[(x-50)2-22500],
∴当x=50时,销售额y最大,为$\frac{9a}{8}$,
于是该商品的价格上涨50%才能使销售的总金额最大.
点评 本题考查函数模型的选择与应用,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.设|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,∠BAC=60°,$\overrightarrow{CD}$=2$\overrightarrow{BC}$,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+(1-x)$\overrightarrow{AB}$,x∈[0,1],则$\overrightarrow{AE}$在$\overrightarrow{AC}$上的投影的取值范围是( )
| A. | [0,1] | B. | [1,7] | C. | [7,9] | D. | [9,21] |
7.若a≤1,则$\sqrt{(a-1)^{2}}$化简后为( )
| A. | a-1 | B. | 1-a | C. | a+1 | D. | -a-1 |
14.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,a2=4,设数列{an}的前n项和为Sn,则数列{$\frac{1}{{S}_{n}}$}的前10项和为( )
| A. | $\frac{11}{12}$ | B. | $\frac{10}{11}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
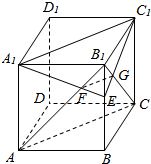 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.