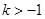题目内容
某同学为了研究函数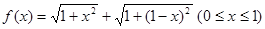 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为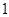 的正方形
的正方形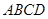 和
和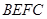 ,点
,点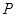 是边
是边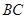 上的一个动点,设
上的一个动点,设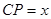 ,则
,则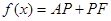 .那么可推知方程
.那么可推知方程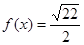 解的个数是( )
解的个数是( )
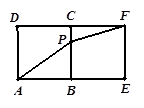
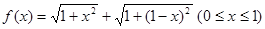 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为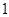 的正方形
的正方形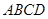 和
和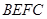 ,点
,点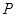 是边
是边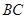 上的一个动点,设
上的一个动点,设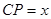 ,则
,则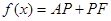 .那么可推知方程
.那么可推知方程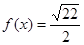 解的个数是( )
解的个数是( )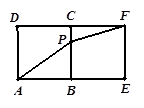
A. . . | B.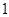 . . | C.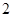 . . | D.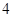 . . |
C
试题分析:从图中知
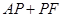 的最小值是
的最小值是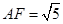 (当
(当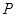 是
是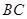 中点
中点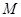 时取得),最大值是
时取得),最大值是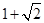 (当
(当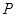 与
与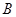 或
或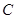 重合时取得),当
重合时取得),当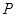 从点
从点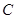 运动到点
运动到点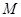 时
时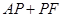 在递减,当
在递减,当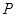 从点
从点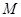 运动到点
运动到点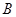 时
时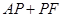 在递增,
在递增,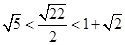 ,故使
,故使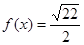 成立的
成立的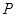 点有两个,即方程有两解.
点有两个,即方程有两解.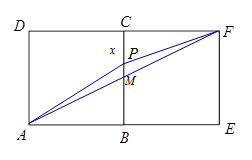

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
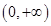 上的函数
上的函数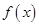 ,如果对任意
,如果对任意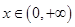 ,恒有
,恒有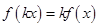 (
(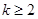 ,
,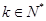 )成立,则称
)成立,则称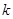 阶缩放函数.
阶缩放函数.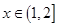 时,
时,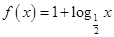 ,求
,求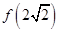 的值;
的值;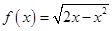 ,求证:函数
,求证:函数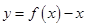 在
在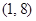 上无零点;
上无零点;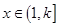 时,
时,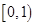 ,求
,求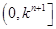 (
(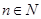 )上的取值范围.
)上的取值范围.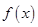 对任意
对任意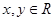 ,都有
,都有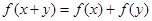 ,当
,当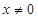 时,
时,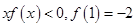
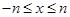 时
时 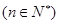 ,
,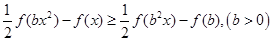
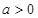 ,
,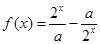 是
是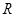 上的奇函数.
上的奇函数.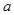 的值;
的值;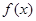 在
在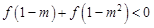 .
.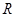 的函数
的函数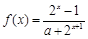 是奇函数.
是奇函数.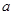 的值
的值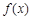 的单调性;
的单调性;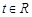 ,不等式
,不等式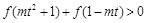 恒成立,求实数
恒成立,求实数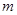 的取值范围.
的取值范围.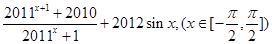 的最大值为
的最大值为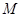 ,最小值为
,最小值为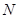 ,
,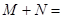 .
.  的定义域为R,若存在常数m>0,使
的定义域为R,若存在常数m>0,使 对一切实数x均成立,则称
对一切实数x均成立,则称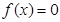 ;②
;② ;③
;③ ;④
;④ ;
; .其中是F函数的序号为______.
.其中是F函数的序号为______.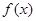 在区间
在区间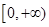 单调增加,则满足
单调增加,则满足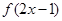 <
<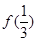 的
的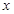 取值范围是( )
取值范围是( )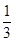 ,
,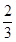 )
)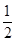 ,
,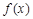 的定义域为
的定义域为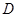 ,若
,若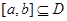 ,使
,使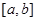 上的值域为
上的值域为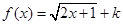 为闭函数,那么
为闭函数,那么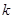 的取值范围是( )
的取值范围是( )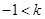 ≤
≤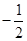
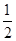 ≤
≤