题目内容
已知椭圆 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.(I)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,
线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.

【答案】分析:(1)欲求圆的方程,关键是确定圆的圆心和半径,因为点O、F都在x轴上,所以圆心必在线段OF的垂直平分线上即在平行于y轴的直线上,结合圆与左准线l相切,可求得半径,进而求得圆心坐标;
(2)欲求点G横坐标的取值范围,从函数思想的角度考虑,先将其表示成某一变量的函数,后求函数的值域,这里取直线AB的斜率K为自变量,通过解方程组求得点G横坐标(用k表示),再求其取值范围.
解答: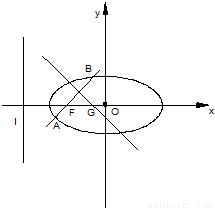 解:(I)∵a2=2,b2=1,
解:(I)∵a2=2,b2=1,
∴c=1,F(-1,0),l:x=-2.
∵圆过点O、F,
∴圆心M在直线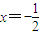 上.
上.
设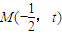 ,则圆半径
,则圆半径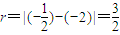 .
.
由|OM|=r,得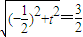 ,
,
解得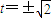 .
.
∴所求圆的方程为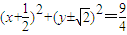 .
.
(II)设直线AB的方程为y=k(x+1)(k≠0),
代入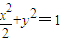 ,整理得(1+2k2)x2+4k2x+2k2-2=0.
,整理得(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x,y),
则 ,
,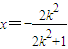 ,
,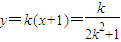
∴AB的垂直平分线NG的方程为 .
.
令y=0,得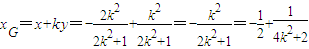 .
.
∵k≠0,∴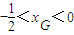 ,
,
∴点G横坐标的取值范围为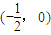 .
.
点评:本小题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力,直线与圆锥曲线的位置关系问题,通常是先联立组成方程组,消去x(或y),得到y(或x)的方程.我们在研究圆锥曲线时,经常涉及到直线与圆锥曲线的位置关系的研究.主要涉及到:交点问题、弦长问题、弦中点(中点弦)等问题,常用的方法:联立方程组,借助于判别式,数形结合法等.
(2)欲求点G横坐标的取值范围,从函数思想的角度考虑,先将其表示成某一变量的函数,后求函数的值域,这里取直线AB的斜率K为自变量,通过解方程组求得点G横坐标(用k表示),再求其取值范围.
解答:
 解:(I)∵a2=2,b2=1,
解:(I)∵a2=2,b2=1,∴c=1,F(-1,0),l:x=-2.
∵圆过点O、F,
∴圆心M在直线
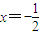 上.
上.设
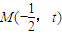 ,则圆半径
,则圆半径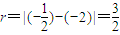 .
.由|OM|=r,得
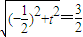 ,
,解得
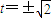 .
.∴所求圆的方程为
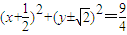 .
.(II)设直线AB的方程为y=k(x+1)(k≠0),
代入
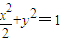 ,整理得(1+2k2)x2+4k2x+2k2-2=0.
,整理得(1+2k2)x2+4k2x+2k2-2=0.∵直线AB过椭圆的左焦点F,∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x,y),
则
 ,
,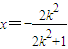 ,
,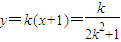
∴AB的垂直平分线NG的方程为
 .
.令y=0,得
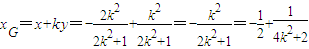 .
.∵k≠0,∴
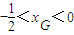 ,
,∴点G横坐标的取值范围为
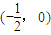 .
.点评:本小题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力,直线与圆锥曲线的位置关系问题,通常是先联立组成方程组,消去x(或y),得到y(或x)的方程.我们在研究圆锥曲线时,经常涉及到直线与圆锥曲线的位置关系的研究.主要涉及到:交点问题、弦长问题、弦中点(中点弦)等问题,常用的方法:联立方程组,借助于判别式,数形结合法等.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.
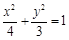 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C, ,其中圆心P的坐标为
,其中圆心P的坐标为 .
. ,求
,求 上,求椭圆的方程.
上,求椭圆的方程. 的左焦点为F,右顶点为A,点B在椭圆上,且
的左焦点为F,右顶点为A,点B在椭圆上,且 轴,直线AB交
轴,直线AB交 轴于点P。若
轴于点P。若 ,则椭圆的离心率为
,则椭圆的离心率为