题目内容
10.已知$\frac{4sinα+2cosα}{5cosα+3sinα}$=2.(1)求tan(90°+α)的值;
(2)求sin2α-sinαcosα-2cos2α的值.
分析 (1)由条件利用同角三角函数的基本关系求得tanα的值,再利用诱导公式求得tan(90°+α)的值.
(2)利用同角三角函数的基本关系把要求的式子化为 $\frac{{tan}^{2}α-tanα-2}{{tan}^{2}α+1}$,从而利用(1)的结论求得它的值.
解答 解:(1)∵$\frac{4sinα+2cosα}{5cosα+3sinα}$=$\frac{4tanα+2}{5+3tanα}$=2,∴tanα=-4,
∴tan(90°+α)=-cotα=$\frac{1}{4}$.
(2)sin2α-sinαcosα-2cos2α=$\frac{{sin}^{2}α-sinαcosα-{2cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{{tan}^{2}α-tanα-2}{{tan}^{2}α+1}$=$\frac{16+4-2}{16+1}$=$\frac{18}{17}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
20. 已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
 已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向左平移$\frac{5π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{5π}{12}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |
5.已知函数y=3|x|在区间[a,b]上的值域为[1,9],则a2+b2-2a的取值范围是( )
| A. | {4,12} | B. | {8,12} | C. | [4,12] | D. | [8,12] |
15.正方体ABCD-A1B1C1D1的棱长为1,M是棱AB的中点,点P是平面ABCD上的动点,P到直线A1D1的距离为d,且d2-|PM|2=1,则动点P的轨迹是( )
| A. | 圆 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线 |
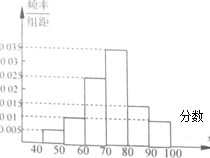 对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.
对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.