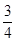题目内容
已知函数f（x）=ax3+bx2+cx+d是R上的奇函数，且在x=1时取得极小值-
．
（1）求函数f（x）的解析式；
（2）对任意x1，x2∈[-1，1]，证明：f（x1）-f（x2）≤
．
| 2 |
| 3 |
（1）求函数f（x）的解析式；
（2）对任意x1，x2∈[-1，1]，证明：f（x1）-f（x2）≤
| 4 |
| 3 |
（1）可知b=d=0，（2分）
所以f′（x）=3ax2+c
可知
⇒
⇒
，
经检验知：f（x）=
x3-x（4分）
（2）即证f（x）max-f（x）min≤
（6分）
因为f′（x）=x2-1，所以x∈[-1，1]时f′（x）≤0，从而函数f（x）在[-1，1]上单调递减，
所以f（x）max=f（-1）=
，f（x）min=f（1）=-
，
所以f（x）max-f（x）min≤
，
从而对任意x1，x2∈[-1，1]，有f（x1）-f（x2）≤
，（10分）
所以f′（x）=3ax2+c
可知
|
|
|
经检验知：f（x）=
| 1 |
| 3 |
（2）即证f（x）max-f（x）min≤
| 4 |
| 3 |
因为f′（x）=x2-1，所以x∈[-1，1]时f′（x）≤0，从而函数f（x）在[-1，1]上单调递减，
所以f（x）max=f（-1）=
| 2 |
| 3 |
| 2 |
| 3 |
所以f（x）max-f（x）min≤
| 4 |
| 3 |
从而对任意x1，x2∈[-1，1]，有f（x1）-f（x2）≤
| 4 |
| 3 |
练习册系列答案
相关题目
( )
