题目内容
已知函数f(x)=alnx+x2(a为实常数).
(1)当a=-4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1,x2∈[1,e],都有|f(x1)-f(x2)|≤|
-
|,求实数a的取值范围.
(1)当a=-4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1,x2∈[1,e],都有|f(x1)-f(x2)|≤|
| 1 |
| x1 |
| 1 |
| x2 |
(1)当a=-4时,f(x)=-4lnx+x2,函数的定义域为(0,+∞).
f′(x)=-
+2x=
.
当x∈[1,
)时,f′(x)0,
所以函数f(x)在[1,
)上为减函数,在(
,e]上为增函数,
由f(1)=-4ln1+12=1,f(e)=-4lne+e2=e2-4,
所以函数f(x)在[1,e]上的最大值为e2-4,相应的x值为e;
(2)由f(x)=alnx+x2,得f′(x)=
+2x=
.
若a≥0,则在[1,e]上f′(x)>0,函数f(x)=alnx+x2在[1,e]上为增函数,
由f(1)=1>0知,方程f(x)=0的根的个数是0;
若a<0,由f′(x)=0,得x=-
(舍),或x=
.
若
≤1,即-2≤a<0,f(x)=alnx+x2在[1,e]上为增函数,
由f(1)=1>0知,方程f(x)=0的根的个数是0;
若
≥e,即a≤-2e2,f(x)=alnx+x2在[1,e]上为减函数,
由f(1)=1,f(e)=alne+e2=e2+a≤-e2<0,
所以方程f(x)=0在[1,e]上有1个实数根;
若1<
<e,即-2e2<a<-2,
f(x)在[1,
]上为减函数,在[
,e]上为增函数,
由f(1)=1>0,f(e)=e2+a.
f(x)min=f(
)=
ln(-
)-
=
[ln(-
)-1].
当-
<e,即-2e<a<-2时,f(
)>0,方程f(x)=0在[1,e]上的根的个数是0.
当a=-2e时,方程f(x)=0在[1,e]上的根的个数是1.
当-e2≤a<-2e时,f(
)<0,f(e)=a+e2≥0,方程f(x)=0在[1,e]上的根的个数是2.
当-2e2<a<-e2时,f(
)<0,f(e)=a+e2<0,方程f(x)=0在[1,e]上的根的个数是1;
(3)若a>0,由(2)知函数f(x)=alnx+x2在[1,e]上为增函数,
不妨设x1<x2,则|f(x1)-f(x2)|≤|
-
|变为f(x2)+
<f(x1)+
,由此说明函数G(x)=f(x)+
在[1,e]单调递减,所以G′(x)=
+2x-
≤0对x∈[1,e]恒成立,即a≤-2x2+
对x∈[1,e]恒成立,
而-2x2+
在[1,e]单调递减,所以a≤-2e2+
.
所以,满足a>0,且对任意的x1,x2∈[1,e],都有|f(x1)-f(x2)|≤|
-
|成立的实数a的取值范围不存在.
f′(x)=-
| 4 |
| x |
2(x+
| ||||
| x |
当x∈[1,
| 2 |
所以函数f(x)在[1,
| 2 |
| 2 |
由f(1)=-4ln1+12=1,f(e)=-4lne+e2=e2-4,
所以函数f(x)在[1,e]上的最大值为e2-4,相应的x值为e;
(2)由f(x)=alnx+x2,得f′(x)=
| a |
| x |
| 2x2+a |
| x |
若a≥0,则在[1,e]上f′(x)>0,函数f(x)=alnx+x2在[1,e]上为增函数,
由f(1)=1>0知,方程f(x)=0的根的个数是0;
若a<0,由f′(x)=0,得x=-
-
|
-
|
若
-
|
由f(1)=1>0知,方程f(x)=0的根的个数是0;
若
-
|
由f(1)=1,f(e)=alne+e2=e2+a≤-e2<0,
所以方程f(x)=0在[1,e]上有1个实数根;
若1<
-
|
f(x)在[1,
-
|
-
|
由f(1)=1>0,f(e)=e2+a.
f(x)min=f(
-
|
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
当-
| a |
| 2 |
-
|
当a=-2e时,方程f(x)=0在[1,e]上的根的个数是1.
当-e2≤a<-2e时,f(
-
|
当-2e2<a<-e2时,f(
-
|
(3)若a>0,由(2)知函数f(x)=alnx+x2在[1,e]上为增函数,
不妨设x1<x2,则|f(x1)-f(x2)|≤|
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x |
| a |
| x |
| 1 |
| x2 |
| 1 |
| x |
而-2x2+
| 1 |
| x |
| 1 |
| e |
所以,满足a>0,且对任意的x1,x2∈[1,e],都有|f(x1)-f(x2)|≤|
| 1 |
| x1 |
| 1 |
| x2 |

练习册系列答案
相关题目
 ,
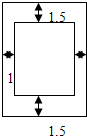
, ,
, ,则
,则 的大小关系是( ).
的大小关系是( ).