题目内容
16.已知f(x)=a+lnx,记g(x)=f′(x),h(x)=f(x)•g(x).(1)已知函数h(x)在[1,+∞)上单调递减,求实数a的取值范围;
(2)①求证:当a=1时,f(x)≤x;
②当a=2时,若不等式h(x)≥tg(x+1)(x∈[1,+∞))恒成立,求实数t的取值范围.
分析 (1)求出导数,由题意可得h′(x)≤0恒成立.即有1-a≤lnx在x≥1恒成立,求得右边函数的最小值即可;
(2)①令函数y=1+lnx-x,求出导数,判断单调性,即可得证;
②当a=2时,不等式h(x)≥tg(x+1)(x∈[1,+∞))恒成立即为t≤(1+$\frac{1}{x}$)(2+lnx)在x∈[1,+∞)恒成立.令函数y=(1+$\frac{1}{x}$)(2+lnx),求得导数,判断单调性,可得最小值,即可得到所求范围.
解答 解:(1)g(x)=f′(x)=$\frac{1}{x}$,
h(x)=f(x)•g(x)=(a+lnx)•$\frac{1}{x}$,
h′(x)=$\frac{1}{{x}^{2}}$-(a+lnx)•$\frac{1}{{x}^{2}}$,
由题意可得h′(x)≤0恒成立.
即有1-a≤lnx在x≥1恒成立,由lnx≥0,
则1-a≤0,即为a≥1;
(2)①证明:令函数y=1+lnx-x,
y′=$\frac{1}{x}$-1=$\frac{1-x}{x}$,
当x>1时,y′<0,函数y递减;当0<x<1时,y′>0,函数y递增.
即有x=1处取得极大值,也为最大值,且为0,
则1+lnx-x≤0,
则f(x)≤x;
②当a=2时,不等式h(x)≥tg(x+1)(x∈[1,+∞))恒成立即为
t≤(1+$\frac{1}{x}$)(2+lnx)在x∈[1,+∞)恒成立.
令函数y=(1+$\frac{1}{x}$)(2+lnx),则y′=$\frac{x-1-lnx}{{x}^{2}}$,
由x≥1时,x-1≥lnx成立,可得y′≥0,函数y递增.
则函数y的最小值为4.
则t≤4.
点评 本题考查导数的运用:求单调区间和极值、最值,考查函数单调性的运用,提示考查不等式恒成立思想,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y | B. | x | C. | 5 | D. | $\frac{1}{5}$ |
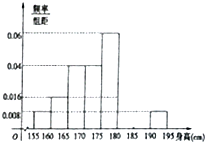 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人,则第七组的频率为( )
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人,则第七组的频率为( )