题目内容
(本小题满分12分)如图,在四棱锥P—ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA//平面BDM,
(1)求证:M为PC的中点;
(2)求证:面ADM⊥面PBC。
(1)求证:M为PC的中点;
(2)求证:面ADM⊥面PBC。

(Ⅰ)见解析 (Ⅱ) 见解析
(1):连接AC,AC与BD交于G,则面PAC∩面BDM=MG,
由PA//平面BDM,可得PA//MG……3分∵底面ABCD为菱形,∴G为AC的中点,
∴MG为△PAC的中位线。因此M为PC的中点。……5分
(2)取AD中点O,连结PO,BO。∵△PAD是正三角形,∴PO⊥AD,
又因为平面PAD⊥平面ABCD,所以,PO⊥平面ABCD,…7分
∵底面ABCD是菱形且∠BAD=60°,△ABD是正三角形,
∴AD⊥OB。∴OA,OB,OP两两垂直,建立空间直角坐标系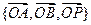 …7分
…7分
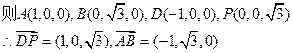
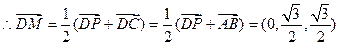 ………………9分
………………9分
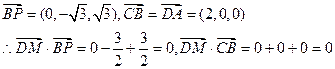
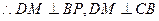 ……11分∴DM⊥平面PBC,又DM
……11分∴DM⊥平面PBC,又DM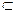 平面ADM,
平面ADM,
∴ADM⊥面PBC …12分
注:其他方法参照给分。

由PA//平面BDM,可得PA//MG……3分∵底面ABCD为菱形,∴G为AC的中点,
∴MG为△PAC的中位线。因此M为PC的中点。……5分
(2)取AD中点O,连结PO,BO。∵△PAD是正三角形,∴PO⊥AD,
又因为平面PAD⊥平面ABCD,所以,PO⊥平面ABCD,…7分
∵底面ABCD是菱形且∠BAD=60°,△ABD是正三角形,
∴AD⊥OB。∴OA,OB,OP两两垂直,建立空间直角坐标系
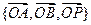 …7分
…7分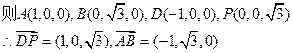
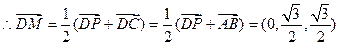 ………………9分
………………9分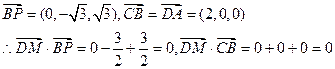
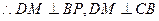 ……11分∴DM⊥平面PBC,又DM
……11分∴DM⊥平面PBC,又DM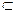 平面ADM,
平面ADM,∴ADM⊥面PBC …12分
注:其他方法参照给分。


练习册系列答案
相关题目
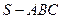 中,
中,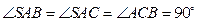 ,
, .
. ;
;
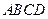 所在平面与圆
所在平面与圆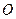 所在平面相交于
所在平面相交于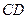 ,线段
,线段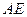 垂直于圆
垂直于圆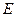 是圆
是圆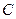 、
、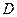 的点,
的点,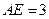 ,圆
,圆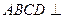 平面
平面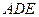 ;
;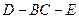 的平面角的正切值.
的平面角的正切值.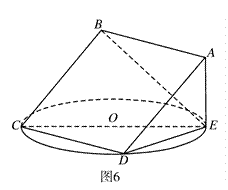
 (如图)底面是边长为2的正方形.侧棱
(如图)底面是边长为2的正方形.侧棱 底面
底面 ,
, 、
、 分别为
分别为 、
、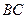 的中点,
的中点,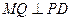 于
于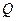 。
。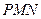 ⊥平面
⊥平面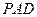 ;
;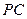 与平面
与平面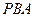 所成角的正弦值为
所成角的正弦值为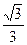 ,求PA的长;
,求PA的长;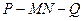 的余弦值。
的余弦值。
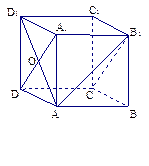
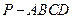 中,
中,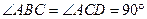 ,
,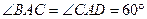 ,
,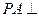 底面
底面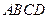 ,
,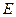 为
为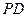 的中点,
的中点,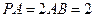 .
.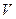 ;
;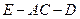 的大小.
的大小.
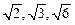 ,这个长方体对角线的长是( )
,这个长方体对角线的长是( )