题目内容
(本小题满分13分)已知直四棱柱ABCD—A1B1C1D1的
底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,
M为线段AC1的中点. (1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1;
(3)求平面AFC1与与平面ABCD所成二面角的大小.
底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,
M为线段AC1的中点. (1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1;
(3)求平面AFC1与与平面ABCD所成二面角的大小.
(Ⅰ) 见解析 (Ⅱ)见解析 (Ⅲ)30°或150°
法一:
(1)延长C1F交CB的延长线于点N,连接AN。因为F是BB1的中点,
 所以F为C1N的中点,B为CN的中点。····2分
所以F为C1N的中点,B为CN的中点。····2分
又M是线段AC1的中点,故MF∥AN。·····3分
又MF 平面ABCD,AN
平面ABCD,AN 平面ABCD。
平面ABCD。
∴MF∥平面ABCD。 ···5分
(2)证明:连BD,由直四棱柱ABCD—A1B1C1D1
可知A1A⊥平面ABCD,又∵BD 平面ABCD,
平面ABCD,
∴A1A⊥BD。∵四边形ABCD为菱形,∴AC⊥BD。
又∵AC∩A1A=A,AC,AA 平面ACC1A1。
平面ACC1A1。
∴BD⊥平面ACC1A1。 ·················7分
在四边形DANB中,DA∥BN且DA=BN,所以四边形DANB为平行四边形
故NA∥BD,∴NA⊥平面ACC1A1,又因为NA 平面AFC1
平面AFC1
∴平面AFC1⊥ACC1A1
(3)由(2)知BD⊥ACC1A1,又AC1 ACC1A1,∴BD⊥AC1,∴BD∥NA,∴AC1⊥NA。
ACC1A1,∴BD⊥AC1,∴BD∥NA,∴AC1⊥NA。
又由BD⊥AC可知NA⊥AC,
∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角。···10分
在Rt△C1AC中,tan ,故∠C1AC=30°···12分
,故∠C1AC=30°···12分
∴平面AFC1与平面ABCD所成二面角的大小为30°或150°。···13分
(1)延长C1F交CB的延长线于点N,连接AN。因为F是BB1的中点,
 所以F为C1N的中点,B为CN的中点。····2分
所以F为C1N的中点,B为CN的中点。····2分又M是线段AC1的中点,故MF∥AN。·····3分
又MF
 平面ABCD,AN
平面ABCD,AN 平面ABCD。
平面ABCD。∴MF∥平面ABCD。 ···5分
(2)证明:连BD,由直四棱柱ABCD—A1B1C1D1
可知A1A⊥平面ABCD,又∵BD
 平面ABCD,
平面ABCD,∴A1A⊥BD。∵四边形ABCD为菱形,∴AC⊥BD。
又∵AC∩A1A=A,AC,AA
 平面ACC1A1。
平面ACC1A1。∴BD⊥平面ACC1A1。 ·················7分
在四边形DANB中,DA∥BN且DA=BN,所以四边形DANB为平行四边形
故NA∥BD,∴NA⊥平面ACC1A1,又因为NA
 平面AFC1
平面AFC1∴平面AFC1⊥ACC1A1
(3)由(2)知BD⊥ACC1A1,又AC1
 ACC1A1,∴BD⊥AC1,∴BD∥NA,∴AC1⊥NA。
ACC1A1,∴BD⊥AC1,∴BD∥NA,∴AC1⊥NA。又由BD⊥AC可知NA⊥AC,
∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角。···10分
在Rt△C1AC中,tan
 ,故∠C1AC=30°···12分
,故∠C1AC=30°···12分∴平面AFC1与平面ABCD所成二面角的大小为30°或150°。···13分

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的三视图如图所示,
的三视图如图所示, ,A1A=
,A1A= ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, 在线段
在线段 上且
上且 =
= .
. ⊥平面
⊥平面 ;
; 的余弦值.
的余弦值.

 中,底面
中,底面 是边长为2的菱形,且
是边长为2的菱形,且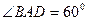 ,
, 为正三角形,
为正三角形, 为
为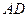 的中点,
的中点, 为棱
为棱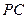 的中点
的中点 平面
平面
 的大小
的大小
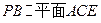 ;
; ;
;  的体积.
的体积.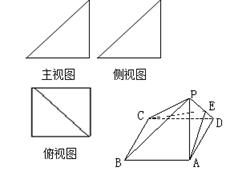
 如图,四棱柱ABCD—A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与BD的交点.
如图,四棱柱ABCD—A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与BD的交点.