题目内容
已知O是坐标原点,点A(1,-1),若点P(x,y)为平面区域
上的一个动点,则
•
的最小值是
|
| OA |
| OP |
-1
-1
.分析:作出不等式组
表示的平面区域,计算
•
=x-y,将直线l:z=x-y进行平移,可得当l经过点D(0,1)时,x-y有最小值,由此可得
•
的最小值.
|
| OA |
| OP |
| OA |
| OP |
解答: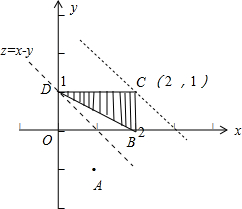 解:作出不等式组
解:作出不等式组
表示的平面区域,如图所示:为一个直角三角形BCD内部及边界.
由于 点A(1,-1),若点P(x,y)为平面区域内的一个动点,则
•
=(1,-1)•(x,y)=x-y.
将直线l:z=x-y进行平移,可得当l经过点D(0,1)时,x-y有最小值-1,
故答案为-1.
 解:作出不等式组
解:作出不等式组
|
由于 点A(1,-1),若点P(x,y)为平面区域内的一个动点,则
| OA |
| OP |
将直线l:z=x-y进行平移,可得当l经过点D(0,1)时,x-y有最小值-1,
故答案为-1.
点评:本题主要考查两个向量的数量积的运算,以及简单的线性规划问题,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知O是坐标原点,点A(-1,1),若点M(x,y)为平面区域
,上的一个动点,则
•
的取值范围是( )
|
| OA |
| OM |
| A、[-1,0] |
| B、[0,1] |
| C、[0,2] |
| D、[-1,2] |