题目内容
给定两个命题,P:关于x的方程x2-x+a=0有实数根;Q:对任意实数x都有ax2+ax+1>0(a≠0)恒成立;如果P且Q是假命题、P或Q是真命题,求实数a的取值范围.
关于x的方程x2-x+a=0有实数根?1-4a≥0?a≤
;…(2分)
对任意实数x都有ax2+ax+1>0恒成立?a=0或
?0≤a<4…(5分)
如果P正确,且Q不正确,有0≤a<4,且a>
∴
<a<4;…(8分)
如果Q正确,且P不正确,有a<0或a≥4,且a≤
∴a<0.…(11分)
所以实数a的取值范围为(-∞,0)∪(
,4)…(12分)
| 1 |
| 4 |
对任意实数x都有ax2+ax+1>0恒成立?a=0或
|
如果P正确,且Q不正确,有0≤a<4,且a>
| 1 |
| 4 |
| 1 |
| 4 |
如果Q正确,且P不正确,有a<0或a≥4,且a≤
| 1 |
| 4 |
所以实数a的取值范围为(-∞,0)∪(
| 1 |
| 4 |

练习册系列答案
相关题目
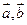 都是非零向量,那么命题“
都是非零向量,那么命题“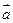 与
与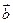 共线”是命题“
共线”是命题“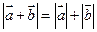 ”的( )
”的( ) 是( )
是( )