题目内容
设函数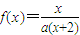 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,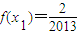 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)(1)求f(x)的表达式;
(2)求x2011的值;
(3)若
 且
且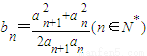 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.
【答案】分析:(1)由方程x=f(x)有唯一解,则ax2+(2a-1)x=0有唯一解,知 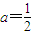 ,由此能求出f(x)的表达式;
,由此能求出f(x)的表达式;
(2)由f(xn)=xn+1,知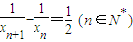 ,由 等差数列的定义可求出数列{xn}的通项公式;
,由 等差数列的定义可求出数列{xn}的通项公式;
(3)由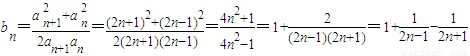
b1+b2+…+bn-n<1,由此能证明b1+b2+…+bn<n+1.
解答:解:(1)由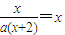 ,可化简为ax(x+2)=x∴ax2+(2a-1)x=0
,可化简为ax(x+2)=x∴ax2+(2a-1)x=0
∴当且仅当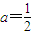 时,方程x=f(x)有唯一解.
时,方程x=f(x)有唯一解.
从而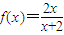
(2)由已知f(xn)=xn+1(n∈N*),得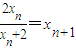
∴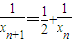 ,即
,即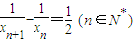
∴数列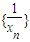 是以
是以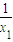 为首项,
为首项, 为公差的等差数列.
为公差的等差数列. ,∴
,∴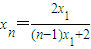
∵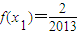 ,
,
∴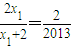 ,即
,即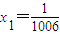
∴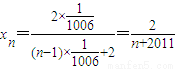
故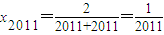
(3)证明:∵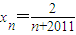 ,
,
∴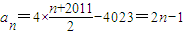 ∴
∴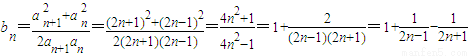
∴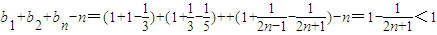
故b1+b2+…+bn<n+1.
点评:本题考查数列的性质和应用,解题时要注意通项公式的求法和裂项公式的合理运用,属于中档题.
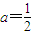 ,由此能求出f(x)的表达式;
,由此能求出f(x)的表达式;(2)由f(xn)=xn+1,知
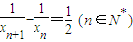 ,由 等差数列的定义可求出数列{xn}的通项公式;
,由 等差数列的定义可求出数列{xn}的通项公式;(3)由
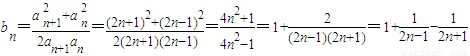
b1+b2+…+bn-n<1,由此能证明b1+b2+…+bn<n+1.
解答:解:(1)由
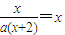 ,可化简为ax(x+2)=x∴ax2+(2a-1)x=0
,可化简为ax(x+2)=x∴ax2+(2a-1)x=0∴当且仅当
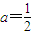 时,方程x=f(x)有唯一解.
时,方程x=f(x)有唯一解.从而
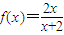
(2)由已知f(xn)=xn+1(n∈N*),得
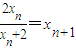
∴
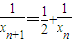 ,即
,即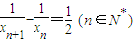
∴数列
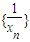 是以
是以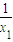 为首项,
为首项, 为公差的等差数列.
为公差的等差数列. ,∴
,∴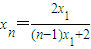
∵
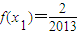 ,
,∴
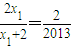 ,即
,即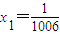
∴
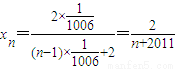
故
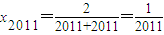
(3)证明:∵
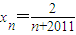 ,
,∴
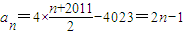 ∴
∴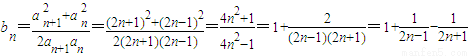
∴
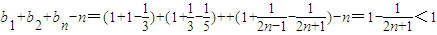
故b1+b2+…+bn<n+1.
点评:本题考查数列的性质和应用,解题时要注意通项公式的求法和裂项公式的合理运用,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
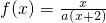 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,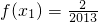 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)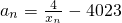 且
且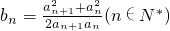 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.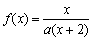 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数, ,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;
,f(xn)=xn+1(n∈N*)。 (1)求f(x)的表达式;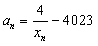 且
且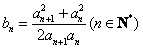 ,求证:
,求证: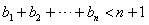 。
。 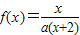 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,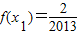 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)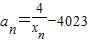 且
且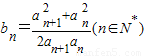 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.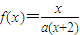 ,方程x=f(x)有唯一解,其中实数a为常数,
,方程x=f(x)有唯一解,其中实数a为常数,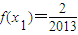 ,f(xn)=xn+1(n∈N*)
,f(xn)=xn+1(n∈N*)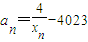 且
且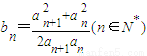 ,求证:b1+b2+…+bn<n+1.
,求证:b1+b2+…+bn<n+1.