题目内容
平行四边形ABCD中，E为CD中点，线段AE与BD相交于点P，记
=a，
=b，则
可以表示为（ ）
| AB |
| AD |
| AP |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析：本题用到教科书的一个例题的结论：在平行四边形ABCD中，E为CD中点，线段AE与BD相交于点P，则可得到点P是BD的三等分点，于是可得结论．
解答：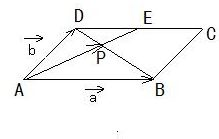
解：如图，易证得点P是对角线BD的三等分点，因此有：
=
+
=
+
=
+
（
-
）=
（
+2
）
故选A
解：如图，易证得点P是对角线BD的三等分点，因此有：| AP |
| AD |
| DP |
| b |
| 1 |
| 3 |
| DB |
| b |
| 1 |
| 3 |
| a |
| b |
| 1 |
| 3 |
| a |
| b |
故选A
点评：本题考查向量的加法运算，以及向量加法的三角形法则和平行四边形法则，共线向量的概念，向量的基底表示，向量相等的概念．
练习册系列答案
相关题目
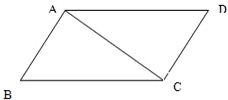如图，在平行四边形ABCD中，AB=AC=1，∠ACD=90°，将它沿对角线AC折起，使AB与CD成60°角，则此时B、D的距离是 （ ）A、2或
| ||
B、2或
| ||
| C、2 | ||
D、1或
|
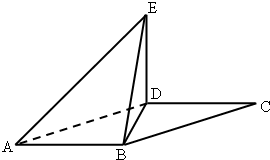如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
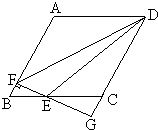如图，在平行四边形ABCD中，AB=4，BC=3，∠BAD=120°，E为BC上一动点（不与B重合），作EF⊥AB于F，FE的延长线交DC的延长线于点G，设BE=x，△DEF的面积为S．