题目内容
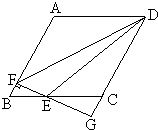 如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.
如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.(1)求证:△BEF∽△CEG;
(2)求用x表示S的函数关系式,并写出x的取值范围;
(3)当E运动到何处时,S有最大值,最大值是多少?
分析:(1)要证明△BEF∽△CEG,只需要证明∠BFG=∠G,且∠BEF=∠CEG,即可;
(2)由(1)知DG为△DEF中EF边上的高,在Rt△BFE中,∠B已知,EF可求;在Rt△CEG中,CE=3-x,则GC可求,
∴DG=GC+CD可求,∴△DEF的面积S可表示出来;
(3)函数S是二次函数,二次项系数a=-
<0,对称轴x=
,易得x=3时,S取最大值,是3
.
(2)由(1)知DG为△DEF中EF边上的高,在Rt△BFE中,∠B已知,EF可求;在Rt△CEG中,CE=3-x,则GC可求,
∴DG=GC+CD可求,∴△DEF的面积S可表示出来;
(3)函数S是二次函数,二次项系数a=-
| ||
| 8 |
| 11 |
| 2 |
| 3 |
解答:(1)证明:∵EF⊥AB,AB∥DC,∴EF⊥DG.∴∠BFG=∠G=90°.
又∵∠BEF=∠CEG,∴△BEF∽△CEG;
(2)解:由(1)得DG为△DEF中EF边上的高,设BE=x,
在Rt△BFE中,∠B=60°,EF=BEsinB=
x.
在Rt△CEG中,CE=3-x,GC=(3-x)cos60°=
,∴DG=DC+GC=
,
∴S=
EF•DG=-
x2+
x,(其中0<x≤3);
(3)解:∵a=-
<0,对称轴x=
>3,∴当0<x≤3时,S随x的增大而增大,
所以,当x=3时,即E与C重合时,取最大值:Smax=3
.
又∵∠BEF=∠CEG,∴△BEF∽△CEG;
(2)解:由(1)得DG为△DEF中EF边上的高,设BE=x,
在Rt△BFE中,∠B=60°,EF=BEsinB=
| ||
| 2 |
在Rt△CEG中,CE=3-x,GC=(3-x)cos60°=
| 3-x |
| 2 |
| 11-x |
| 2 |
∴S=
| 1 |
| 2 |
| ||
| 8 |
11
| ||
| 8 |
(3)解:∵a=-
| ||
| 8 |
| 11 |
| 2 |
所以,当x=3时,即E与C重合时,取最大值:Smax=3
| 3 |
点评:本题考查了相似三角形的证明,三角形的面积公式应用和求二次函数在某一区间上的最值问题,属于中档题.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
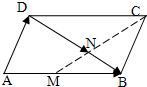 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,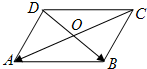 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.