Question

（2012•广州二模）在平行四边形ABCD中，点E是AD的中点，BE与AC相交于点F，若

EF

=m

AB

+n

AD

(m，n∈R)，则

m

n

的值为

-2

．

Answer 1

分析：取BC的中点M，连接DM，交AC于N，由平行四边形ABCD中，点E是AD的中点，BE与AC相交于点F，知AF=FN=CN，故

EF

=

1

3

AB

-

1

6

AD

，由此能求出结果．

解答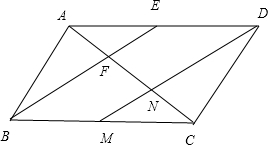：解：取BC的中点M，连接DM，交AC于N，
∵平行四边形ABCD中，点E是AD的中点，BE与AC相交于点F，
∴AF=FN=CN，
∴

EF

=-

1

2

AD

+

1

3

AD

+

1

3

AB

=

1

3

AB

-

1

6

AD

，
∵

EF

=m

AB

+n

AD

(m，n∈R)，
∴m=

1

3

，n=-

1

6

，
∴

m

n

=

1 3

- 1 6

=-2．
故答案为：-2．

点评：本题考查向量的线性运算性质及其几何意义，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．