题目内容
已知数列{an}的前n项和为sn满足sn=
(an+1)2,且an>0.
(1)求数列{an}的通项公式an;
(2)令bn=20-an,求数列{bn}的前n项和Tn的最大值.
| 1 |
| 4 |
(1)求数列{an}的通项公式an;
(2)令bn=20-an,求数列{bn}的前n项和Tn的最大值.
(1)∵sn=
(an+1)2,且an>0.当n≥2时,Sn-1=
(an-1+1)2,
∴an=
(an+1)2-
(an-1+1)2,化为(an+an-1)(an-an-1-2)=0,
∴an-an-1=2.又a1=
(an+1)2,解得a1=1,
∴数列{an}是首项为1,公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
(2)由(1)可得bn=20-an=20-(2n-1)=21-2n.
∴Tn=
=-n2+20n=-(n-10)2+100.
∴当n=10时,Tn取得最大值100.
| 1 |
| 4 |
| 1 |
| 4 |
∴an=
| 1 |
| 4 |
| 1 |
| 4 |
∴an-an-1=2.又a1=
| 1 |
| 4 |
∴数列{an}是首项为1,公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
(2)由(1)可得bn=20-an=20-(2n-1)=21-2n.
∴Tn=
| n(19+21-2n) |
| 2 |
∴当n=10时,Tn取得最大值100.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
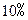 ,这5年的总产是多少?
,这5年的总产是多少? 中,
中, ,
, ,当
,当 时,
时, 等于
等于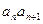 的个位数,若数列
的个位数,若数列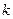 项和为243,则
项和为243,则
 的值是 ( )
的值是 ( ) B
B  C
C  D
D 