题目内容
设向量| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
分析:利用已知条件得出向量的坐标是解决本题的关键,然后利用已知条件向量长度的关系得出x,y的关系式,进而求出点P(x,y)的轨迹方程.
解答:解:由题意得出
=(x+3,y),
=(x-3,y)满足|
|-|
|=2,则得出
-
=2
表示点P(x,y)与点(-3,0)之间的距离减去点P(x,y)与点(3,0)距离的差为2(定植),并且该定值小于点(-3,0)与点(3,0)之间的距离,故该动点P在以点(-3,0)、点(3,0)为焦点的双曲线右支上,并且实轴长为2,因此虚半轴长为
=
,故所求的点P(x,y)的轨迹方程是x2-
=1(x>0)或者(x≥1).
故答案为:x2-
=1(x>0)或者(x≥1).
| a |
| b |
| a |
| b |
| (x+3)2+y2 |
| (x-3)2+y2 |
表示点P(x,y)与点(-3,0)之间的距离减去点P(x,y)与点(3,0)距离的差为2(定植),并且该定值小于点(-3,0)与点(3,0)之间的距离,故该动点P在以点(-3,0)、点(3,0)为焦点的双曲线右支上,并且实轴长为2,因此虚半轴长为
| 32-1 |
| 8 |
| y2 |
| 8 |
故答案为:x2-
| y2 |
| 8 |
点评:本题考查动点轨迹方程的求法,考查学生的转化与化归思想,关键要通过向量坐标得出动点的坐标满足的曲线类型,利用圆锥曲线的定义求出所要求的轨迹方程.

练习册系列答案
相关题目
设向量i、j为直角坐标系的x轴、y轴正方向上的单位向量,若向量
=(x+1)i+yj,
=(x-1)i+yj,且|
|-|
|=1,则满足上述条件的点P(x,y)的轨迹方程是( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 =(x+1)i+yj,
=(x+1)i+yj, =(x-1)i+yj,且|
=(x-1)i+yj,且| |-|
|-| |=1,则满足上述条件的点P(x,y)的轨迹方程是( )
|=1,则满足上述条件的点P(x,y)的轨迹方程是( )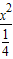 -
- =1(y≥0)
=1(y≥0) -
- =1(x≥0)
=1(x≥0) -
- =1(y≥0)
=1(y≥0) -
- =1(x≥0)
=1(x≥0)